Vilkårlig trekant

En vilkårlig trekant er en trekant, hvor alle sider og vinkler er forskellige, altså hverken retvinklet, ligebenet eller ligesidet.

 

 

Formler og metoder

For at beregne vilkårlige trekanter, skal man bruge cosinus- og sinusrelationerne.

Vær opmærksom på at der ved brug af sinusrelationen kan opstå tvetydighed, i nogle tilfælde findes der to mulige trekanter, der passer til de givne oplysninger og dermed to løsninger.

Læs mere om cosinus- og sinusrelationerne under Trigonometri. 

 

For at kunne beregne en vilkårlig trekant, skal man kende en sidelængde og mindst to andre oplysninger om trekanten.

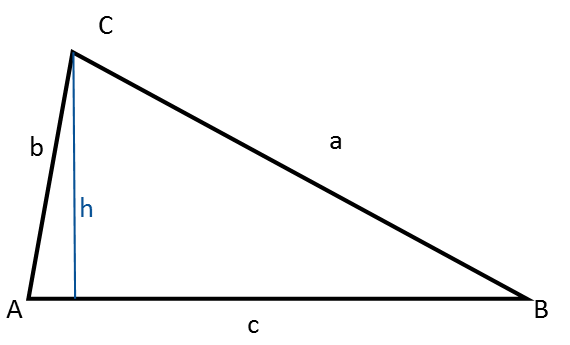
I nogle tilfælde kan trekantens højde bruges i stedet for en sidelængde i beregninger.

 

Bemærk, at trekantens højde opdeler den i to retvinklede trekanter. Det kan være en hjælp i visse beregninger, fordi det gør det muligt at bruge trigonometri for retvinklede trekanter og Pythagoras læresætning.

Men HUSK: Du må ikke bruge formler til retvinklede trekanter, hvis ikke trekanten er retvinklet! 

De må kun bruges, hvis du har opdelt trekanten i to retvinklede trekanter og regner på dem.

 

Til højre kan du finde alle formler til beregning af vilkårlige trekanter.

Regnemaskine

Formler

Side a

$$ a=\frac{h}{sin(B)} $$

$$ a=\frac{c\cdot sin(A)}{sin(C)} $$

$$ a=\frac{b\cdot sin(A)}{sin(B)} $$

$$ a=\sqrt{b^2+c^2-2\cdot b\cdot c\cdot cos(A)} $$

Side b

$$ b=\frac{h}{sin(A)} $$

$$ b=\frac{a\cdot sin(B)}{sin(A)} $$

$$ b=\frac{c\cdot sin(B)}{sin(C)} $$

$$ b=\sqrt{a^2+c^2-2\cdot a\cdot c\cdot cos(B)} $$

Side c

$$ c=\frac{2\cdot Area}{h} $$

$$ c=\frac{b\cdot sin(C)}{sin(B)} $$

$$ c=\frac{a\cdot sin(C)}{sin(A)} $$

$$ c=\sqrt{a^2+b^2-2\cdot a\cdot b\cdot cos(C)} $$

Højde

$$ h=sin(A)\cdot b $$

$$ h=sin(B)\cdot a $$

$$ h=\frac{2\cdot Area}{c} $$

Vinkel A

$$ A=sin^{-1}\biggl(\frac{h}{b}\biggr) $$

$$ A=sin^{-1}\biggl(\frac{a\cdot sin(C)}{c}\biggr) $$

$$ A=sin^{-1}\biggl(\frac{a\cdot sin(B)}{b}\biggr) $$

$$ A=cos^{-1}=\biggl(\frac{b^2+c^2-a^2}{2\cdot b\cdot c}\biggr) $$

Vinkel B

$$ B=sin^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ B=sin^{-1}\biggl(\frac{b\cdot sin(C)}{c}\biggr) $$

$$ B=sin^{-1}\biggl(\frac{b\cdot sin(A)}{a}\biggr) $$

$$ B=cos^{-1}\biggl(\frac{a^2+c^2-b^2}{2\cdot a\cdot c}\biggr) $$

Vinkel C

$$ C = sin^{-1} \biggl( \frac {c \cdot sin(B)}{b} \biggr ) $$

$$ C = sin^{-1} \biggl( \frac {c \cdot sin(A)}{a} \biggr ) $$

$$ C=cos^{-1}\biggl(\frac{a^2+b^2-c^2}{2\cdot a\cdot b}\biggr) $$

Areal

$$ A= \frac{h\cdot c}{2} $$

$$ A= \frac{a\cdot b\cdot sin(C)}{2} $$

$$ A= \frac{a\cdot c\cdot sin(B)}{2} $$

$$ A= \frac{b\cdot c\cdot sin(A)}{2} $$

$$ A= \frac{1}{2} \cdot \sqrt{a^2\cdot c^2 - \biggl( \frac{a^2+c^2-b^2}{2}\biggr)^2} $$

Omkreds

$$ P=a+b+c $$

$$ P=\frac{h}{sin(A)}+\frac{h}{sin(B)}+\frac{h}{tan(A)}+\frac{h}{tan(B)} $$