Ligebenet trekant

En ligebenet trekant har to lige lange sider (ben) og to lige store vinkler, som ligger overfor de to lige lange sider.

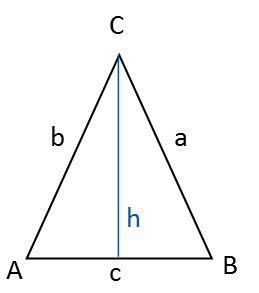
Billede af en ligebenet trekant

Har du kender en af vinklerne samt enten højden eller en af siderne, kan du beregne resten af trekantens sider og vinkler.

Tips til beregning

Hvis du kender den ene vinkel, vil det altid være muligt at regne de to andre ud, fordi summen af alle tre vinkler skal være 180 grader.

Hvis vinkel C er 70 grader, vil vinkel A og B være 55 grader, fordi de de to vinkler er ens.

$$ \angle A+\angle B = 180^\circ - 70^\circ = 110^\circ \\[14pt] $$

$$ \angle A=\angle B=\frac{110^\circ}{2}=55^\circ $$

Hvis vinkel A er 35 grader, så er vinkel B også 35 grader og vinkel C vil være 110 grader fordi:

$35+35+110=180$

Højden fra vinkel C ned til siden c (modstående) deler trekanten i to spejlvendte retvinklede trekanter. Derfor kan du bruge Pythagoras’ sætning og trigonometriske funktioner til beregninger.

Siden c er trekantens grundlinje og vinkel C er dens toppunkt.

Regnemaskine

Formler

Side a

$$ a=b=\frac{h}{sin(A)} $$

$$ a=b=\frac{c}{2\cdot cos(A)} $$

$$ a=b=\frac{h}{cos\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\frac{c}{2\cdot sin\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\sqrt{h^2 + \biggl(\frac{c}{2} \biggr)^2} $$

Side c

$$ c=2\cdot \sqrt{a^2-h^2} $$

$$ c=2\cdot b\cdot cos(A) $$

$$ c=2\cdot b\cdot sin\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot h\cdot tan\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot \frac{h}{tan(A)} $$

Højde

$$ h=b\cdot sin(A) $$

$$ h=\frac{c}{2}\cdot tan(A) $$

$$ h=\frac{c}{tan(C)} $$

$$ h=b\cdot cos\biggl(\frac{\angle C}{2} \biggr) $$

$$ h=\sqrt {b^2-\biggl(\frac{c}{2}\biggr)^2} $$

Vinkel A

$$ A=B=\frac{180-C}{2} $$

$$ A=B=tan^{-1}\biggl(\frac{2\cdot h}{c}\biggr) $$

$$ A=B=sin^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ A=B=cos^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

Vinkel C

$$ C=2\cdot cos^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ C=2\cdot sin^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

$$ C=2\cdot tan^{-1}\biggl(\frac{c}{2\cdot h}\biggr) $$

Areal

$$ A= \frac{h\cdot c}{2} $$

$$ A= \frac{a\cdot b\cdot sin(C)}{2} $$

$$ A= \frac{a\cdot c\cdot sin(B)}{2} $$

$$ A= \frac{b\cdot c\cdot sin(A)}{2} $$

$$ A= \frac{1}{2} \cdot \sqrt{a^2\cdot c^2 - \biggl( \frac{a^2+c^2-b^2}{2}\biggr)^2} $$

Omkreds

$$ P=a+b+c $$

$$ P=\frac{h}{sin(A)}+\frac{h}{sin(B)}+\frac{h}{tan(A)}+\frac{h}{tan(B)} $$