Omskreven cirkel

I alle trekanter kan der tegnes en cirkel, der tangerer trekantens tre vinkelspidser.

 

Den kaldes den omskrevne cirkel

 

 

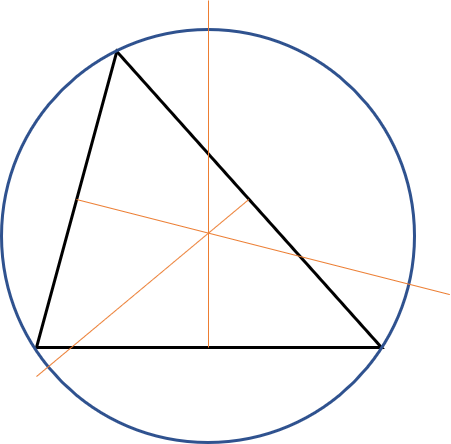
Midtnormaler og centrum

En midtnormal er en vinkelret linie, der deler et liniestykke på midten.

Midtnormalerne deler altså trekantens tre sider (a,b,c) og skærer hinanden i centrum af den omskrevne cirkel.

Hvis du skal tegne en omskreven cirkel, skal du derfor starte med at tegne de tre midtnormaler. I deres skæringspunkt sætter du din passer og kan tegne cirklen.

 

Radius og areal

Radius af den omskrevne cirkel kan beregnes med denne formel:

 

$$ \large r=\frac{a \cdot b \cdot c}{4 \cdot A} $$

 

Hvor \(\large A\) er trekantens areal.

Hvis du skal finde arealet af trekanten, kan du vende formlen om:

 

$$ \large A=\frac{a \cdot b \cdot c}{4 \cdot r} $$

 

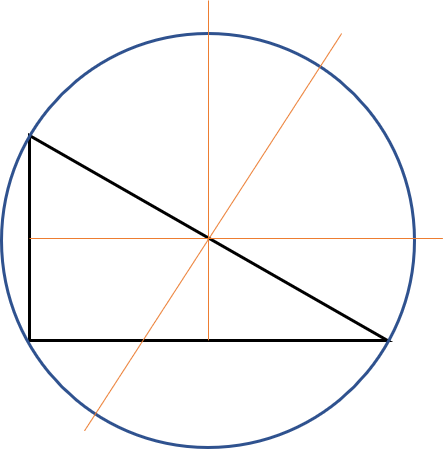
Retvinklet trekant

En retvinklet trekants omskrevne cirkel vil altid have centrum præcis midt på hypotenusen.

Det gør det også lidt nemmere at finde radius, som er det halve af siden c:

 

$$ \large r=\frac{c}{2} $$