Trekanter
Den første polygon.
I plangeometri er trekanten den første polygon. Det er den figur der har færrest kanter.
Trekantens grundelementer
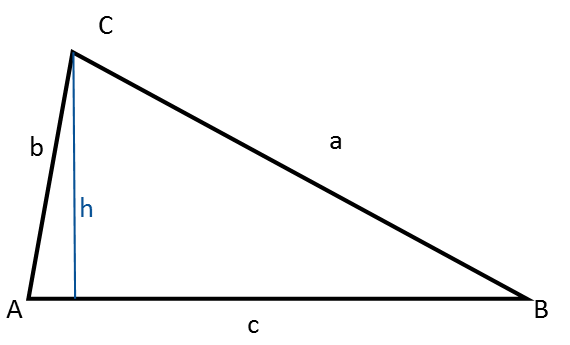
Trekanten har:
- Tre vinkler, som altid betegnes med store bogstaver: A, B, C
- Tre sider, som altid betegnes med små bogstaver: a, b, c
- En vinkelsum på 180°
Højden i en trekant
Højden i en trekant er en linje, der går vinkelret fra en vinkelspids ned på den modstående side (grundlinjen).
Der findes tre højder i en trekant, én for hver side, afhængigt af hvilken der vælges som grundlinje.
Typer af trekanter
Ikke alle trekanter er ens, derfor er nogle også nemmere at beregne end andre.
Trekanter opdeles i forskellige typer, afhængigt af deres sider og vinkler.
Efter vinkler:
- Hvis en af vinklerne er 90°, kalder vi den en Retvinklet Trekant
- Hvis en af vinklerne er over 90°, kalder vi det en Stumpvinklet Trekant
- Hvis alle vinkler er under 90°, kalder vi det en Spidsvinklet Trekant
Efter sider:
- Hvis to af siderne er lige lange, kalder vi den en Ligebenet Trekant
- Hvis alle tre sider er lige lange, kalder vi den en Ligesidet Trekant
Den trekant du ser på figuren herover kaldes en Vilkårlig Trekant.
- Den har ingen vinkler, der er 90°
- Den har ingen sider, der er lige lange.
- Alle vinkler er til gengæld under 90°, så den er også en Spidsvinklet Trekant.
En trekant kan nemlig godt have flere egenskaber. Den kan feks også være både Retvinklet og Ligebenet.
Beregning af trekanter
Mennesker har beregnet trekanter i flere tusinde år.
Allerede de gamle grækere arbejdede med geometri længe før vores tidsregning.
En af de mest kendte var Pythagoras, som formulerede Pythagoras' læresætning, der er en metode til at beregne siderne i en retvinklet trekant.
Senere opstod trigonometri, der er en gren af matematikken, som gør det muligt at beregne vinkler og sider i alle slags trekanter.
Trigonometri blev oprindeligt udviklet af græske astronomer, men er siden blevet videreudviklet af matematikere over hele verden og bruges i dag i alt fra arkitektur til rumfart.