Den retvinklede trekant, har som navnet antyder, altid en ret vinkel.

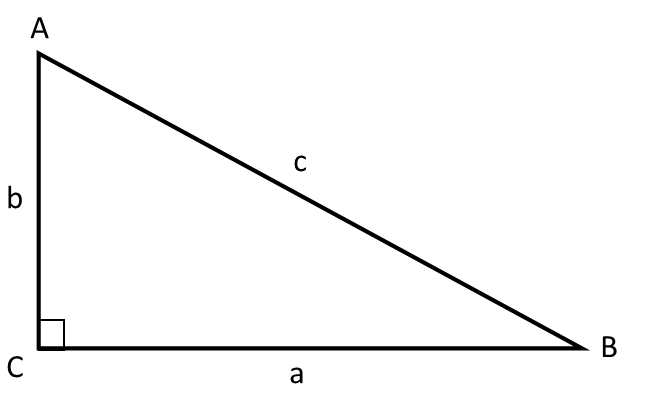
Den rette vinkel hedder vinkel C.

Vinklerne i trekanter benævnes altid med store bogstaver, og siderne med små bogstaver.

Side a og side b kaldes Kateter og danner den rette vinkel.

Side c kaldes Hypotenusen og vil altid være den længste side i trekanten. 

Bemærk at side a ligger overfor vinkel A. 

Det samme gælder for side b og side c og sådan vil det altid være.

Pythagoras læresætning

Pythagoras læresætning beskriver forholdet mellem siderne i en retvinklet trekant.

Pythagoras siger at "kvadratet på side a + kvadratet på side b = kvadratet på side c".

$$ a^2+b^2=c^2 $$

Hvis vi har en trekant hvor \(a=3\) og \(b=4\), får vi følgende:

$$ \begin{align} 3^2 + 4^2 &= c^2 \Leftrightarrow \\ 9 + 16 &= 25 \Leftrightarrow \\ c^2 &= 25 \Leftrightarrow \\ c &= \sqrt{25} = 5 \end{align}$$

Udfra læresætningen kan udledes to formler til at beregne side a og b:

$$ a = \sqrt{c^2-b^2} $$

$$ b = \sqrt{c^2-a^2} $$

Figur

Figuren viser kvadraterne på trekantens sider.

Du kan læse om beregning af vinkler i afsnittet om trigonometri.

Trigonometri og retvinklede trekanter

I afsnittet om Trigonometri kan du læse om Cosinus, Sinus og Tangens.

Cosinus, sinus og tangens kan bruges til, at beregne vinkler og sider i retvinklede trekanter.

HUSK at du ikke må bruge disse formler til trekanter, der ikke er retvinklede.

Til andre trekanter skal du bruge cosinus- og sinus relationerne.

Når vi taler om trekantens sider, taler vi om "hosliggende" og "modstående" kateter.

Hvis du ser på tegningen kan du se, at side b ligger hos vinkel A, så den er hosliggende.

Side a er derimod på modsatte side af vinkel vinkel A, så det er den modstående katete.

Formler

I retvinklede trekanter forholder det sig sådan at:

$$ \cos(v) = \mathit{hosliggende\ katete \over hypotenusen}$$

$$ \sin(v) = \mathit{modstående\ katete \over hypotenusen}$$

$$ \tan(v) = \mathit{modstående\ katete \over hosliggende\ katete}$$

Ved brug af inverse trigonomiske funktioner (arcsin, arccos, arctan), kan man udregne vinklen direkte:

$$ v = \cos^{-1}\biggl(\mathit{hosliggende\ katete \over hypotenusen}\biggr)$$

$$ v = \sin^{-1}\biggl(\mathit{modstående\ katete \over hypotenusen}\biggr)$$

$$ v = \tan^{-1}\biggl(\mathit{modstående\ katete \over hosliggende\ katete}\biggr)$$