El triángulo rectángulo tiene, como su nombre indica, siempre un ángulo recto.

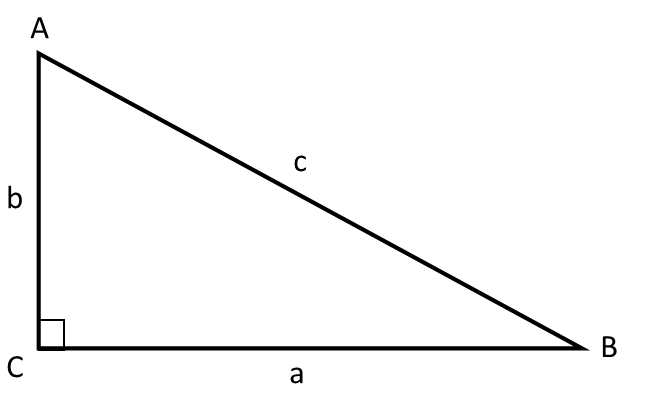
El ángulo recto se llama ángulo C.

Los ángulos de los triángulos se nombran siempre con letras mayúsculas y los lados con letras minúsculas.

Lado a y lado b se llaman catetos y forman el ángulo recto.

Lado c se llama hipotenusa y siempre será el lado más largo del triángulo. 

Observa que lado a está frente a ángulo A. 

Lo mismo ocurre con lado b y lado c, y así será siempre.

Teorema de Pitágoras

El teorema de Pitágoras describe la relación entre los lados de un triángulo rectángulo.

Pitágoras dice que "el cuadrado del lado a + el cuadrado del lado b = el cuadrado del lado c".

$$ a^2 + b^2 = c^2 $$

Si tenemos un triángulo donde \(a = 3\) y \(b = 4\), obtenemos lo siguiente:

$$ \begin{align} 3^2 + 4^2 &= c^2 \Leftrightarrow \\ 9 + 16 &= 25 \Leftrightarrow \\ c^2 &= 25 \Leftrightarrow \\ c &= \sqrt{25} = 5 \end{align} $$

Del teorema se derivan dos fórmulas para calcular los lados a y b:

$$ a = \sqrt{c^2 - b^2} $$

$$ b = \sqrt{c^2 - a^2} $$

Figura

La figura muestra los cuadrados en los lados del triángulo.

Puedes leer sobre el cálculo de ángulos en la sección Trigonometría.

Trigonometría y triángulos rectángulos

En la sección de Trigonometría puedes leer sobre Coseno, Seno y Tangente.

Coseno, seno y tangente pueden usarse para calcular ángulos y lados en triángulos rectángulos.

RECUERDA que no debes usar estas fórmulas para triángulos que no sean rectángulos.

Para otros triángulos debes usar las leyes de cosenos y senos.

Cuando hablamos de los lados del triángulo, nos referimos al cateto "adyacente" y al cateto "opuesto".

Si miras el dibujo puedes ver que lado b está adyacente a ángulo A, por lo que es el cateto adyacente.

Lado a está, en cambio, en el lado opuesto de ángulo A, por lo que es el cateto opuesto.

Fórmulas

En triángulos rectángulos se cumple lo siguiente:

$$ \cos(v) = \frac{\text{cateto adyacente}}{\text{hipotenusa}} $$

$$ \sin(v) = \frac{\text{cateto opuesto}}{\text{hipotenusa}} $$

$$ \tan(v) = \frac{\text{cateto opuesto}}{\text{cateto adyacente}} $$

Mediante el uso de funciones trigonométricas inversas (arcsin, arccos, arctan), puedes calcular el ángulo directamente:

$$ v = \cos^{-1}\biggl(\frac{\text{cateto adyacente}}{\text{hipotenusa}}\biggr) $$

$$ v = \sin^{-1}\biggl(\frac{\text{cateto opuesto}}{\text{hipotenusa}}\biggr) $$

$$ v = \tan^{-1}\biggl(\frac{\text{cateto opuesto}}{\text{cateto adyacente}}\biggr) $$