Triángulos
El primer polígono.
En geometría plana, el triángulo es el primer polígono. Es la figura con menos lados.
Los elementos básicos del triángulo
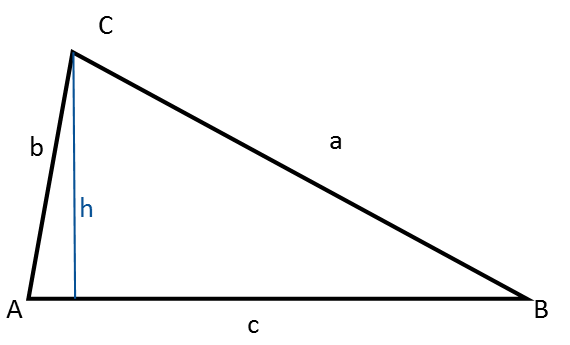
Un triángulo tiene:
- Tres ángulos, siempre designados con letras mayúsculas: A, B, C
- Tres lados, siempre designados con letras minúsculas: a, b, c
- Una suma de ángulos de 180°
La altura en un triángulo
La altura en un triángulo es una línea que va perpendicular desde un vértice hasta el lado opuesto (la base).
Un triángulo tiene tres alturas, una para cada lado, dependiendo de cuál se elija como base.
Tipos de triángulos
No todos los triángulos son iguales, por eso algunos también son más fáciles de calcular que otros.
Los triángulos se dividen en diferentes tipos según sus lados y sus ángulos.
Según los ángulos:
- Si uno de los ángulos es de 90°, lo llamamos un triángulo rectángulo
- Si uno de los ángulos es mayor que 90°, lo llamamos un triángulo obtusángulo
- Si todos los ángulos son menores de 90°, lo llamamos un triángulo acutángulo
Según los lados:
- Si dos lados tienen la misma longitud, lo llamamos un triángulo isósceles
- Si los tres lados tienen la misma longitud, lo llamamos un triángulo equilátero
El triángulo que ves en la figura anterior se llama un triángulo escaleno.
- No tiene ningún ángulo de 90°
- No tiene lados de igual longitud.
- Todos los ángulos son menores de 90°, por lo que también es un triángulo acutángulo
Un triángulo puede tener varias propiedades. Por ejemplo, puede ser rectángulo e isósceles a la vez.
Cálculo de triángulos
Los seres humanos han calculado triángulos durante miles de años.
Ya los antiguos griegos trabajaban con geometría mucho antes de nuestra era.
Uno de los más conocidos fue Pitágoras, quien formuló el teorema de Pitágoras, un método para calcular los lados de un triángulo rectángulo.
Más tarde surgió la trigonometría, una rama de las matemáticas que permite calcular los ángulos y los lados de todo tipo de triángulos.
La trigonometría fue desarrollada originalmente por astrónomos griegos, pero posteriormente ha sido perfeccionada por matemáticos de todo el mundo y hoy se utiliza en campos como la arquitectura y la exploración espacial.