Triángulo escaleno
Un triángulo escaleno es un triángulo donde todos los lados y ángulos son diferentes, es decir, no es rectángulo, isósceles ni equilátero.
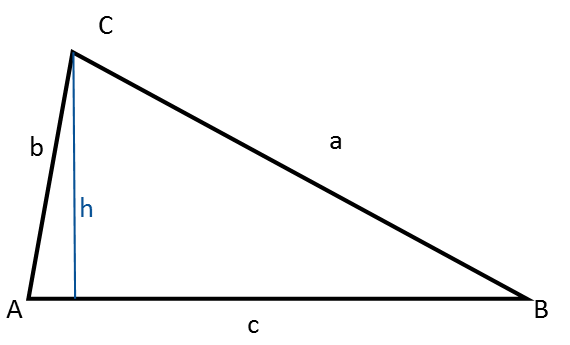
Fórmulas y métodos
Para calcular triángulos escalenos, se deben usar las relaciones del coseno y del seno.
Ten en cuenta que al usar la relación del seno puede surgir ambigüedad, en algunos casos hay dos triángulos posibles que coinciden con los datos dados y, por lo tanto, dos soluciones.
Lee más sobre las relaciones del coseno y del seno en Trigonometría.
Para poder calcular un triángulo escaleno, debes conocer una longitud de lado y al menos otros dos datos sobre el triángulo.
En algunos casos, la altura del triángulo puede usarse en lugar de una longitud de lado en los cálculos.
Observa que la altura del triángulo lo divide en dos triángulos rectángulos. Esto puede ser útil en algunos cálculos porque permite usar la trigonometría de triángulos rectángulos y el teorema de Pitágoras.
Pero RECUERDA: ¡No debes usar fórmulas de triángulos rectángulos si el triángulo no es rectángulo!
Solo se pueden usar si has dividido el triángulo en dos triángulos rectángulos y trabajas con ellos.
A la derecha puedes encontrar todas las fórmulas para calcular triángulos escalenos.