Triángulo isósceles
Un triángulo isósceles tiene dos lados de igual longitud (catetos) y dos ángulos iguales, que están opuestos a los dos lados de igual longitud.
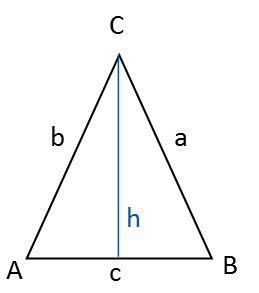
Si conoces uno de los ángulos y la altura o uno de los lados, puedes calcular los lados y ángulos restantes del triángulo.
Consejos para el cálculo
Si conoces uno de los ángulos, siempre es posible calcular los otros dos, porque la suma de los tres ángulos debe ser 180 grados.
Si el ángulo C es de 70 grados, entonces los ángulos A y B serán de 55 grados, porque esos dos ángulos son iguales.
$$ \angle A+\angle B = 180^\circ - 70^\circ = 110^\circ \\[14pt] $$
$$ \angle A=\angle B=\frac{110^\circ}{2}=55^\circ $$
Si el ángulo A es de 35 grados, entonces el ángulo B también es de 35 grados y el ángulo C será de 110 grados porque:
\(35+35+110=180\)
La altura desde el ángulo C hasta el lado c (opuesto) divide el triángulo en dos triángulos rectángulos simétricos. Por eso puedes usar el teorema de Pitágoras y funciones trigonométricas para los cálculos.
El lado c es la base del triángulo y el ángulo C es su vértice.