Números de Fibonacci
Los números de Fibonacci reciben su nombre de Leonardo Fibonacci, un matemático italiano, que describió esta sucesión por primera vez en el año 1202 en el libro Liber Abaci.
Definición recursiva
Los números de Fibonacci se definen mediante una función recursiva:
$$ F_0 = 0, \quad F_1 = 1 $$
$$ F_n = F_{n-1} + F_{n-2} \quad (n \geq 2) $$
Esto significa que cada número de la sucesión es la suma de los dos anteriores.
Los primeros 10 números de Fibonacci son por lo tanto:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 $$
Se puede ver rápidamente el patrón:
$$ 0+1=1,\;\;1+1=2,\;\;1+2=3,\;\;2+3=5,\;\;3+5=8\;\;etc. $$
Los números de Fibonacci pueden ilustrarse con cuadrados cuya longitud de lado corresponde a los números.
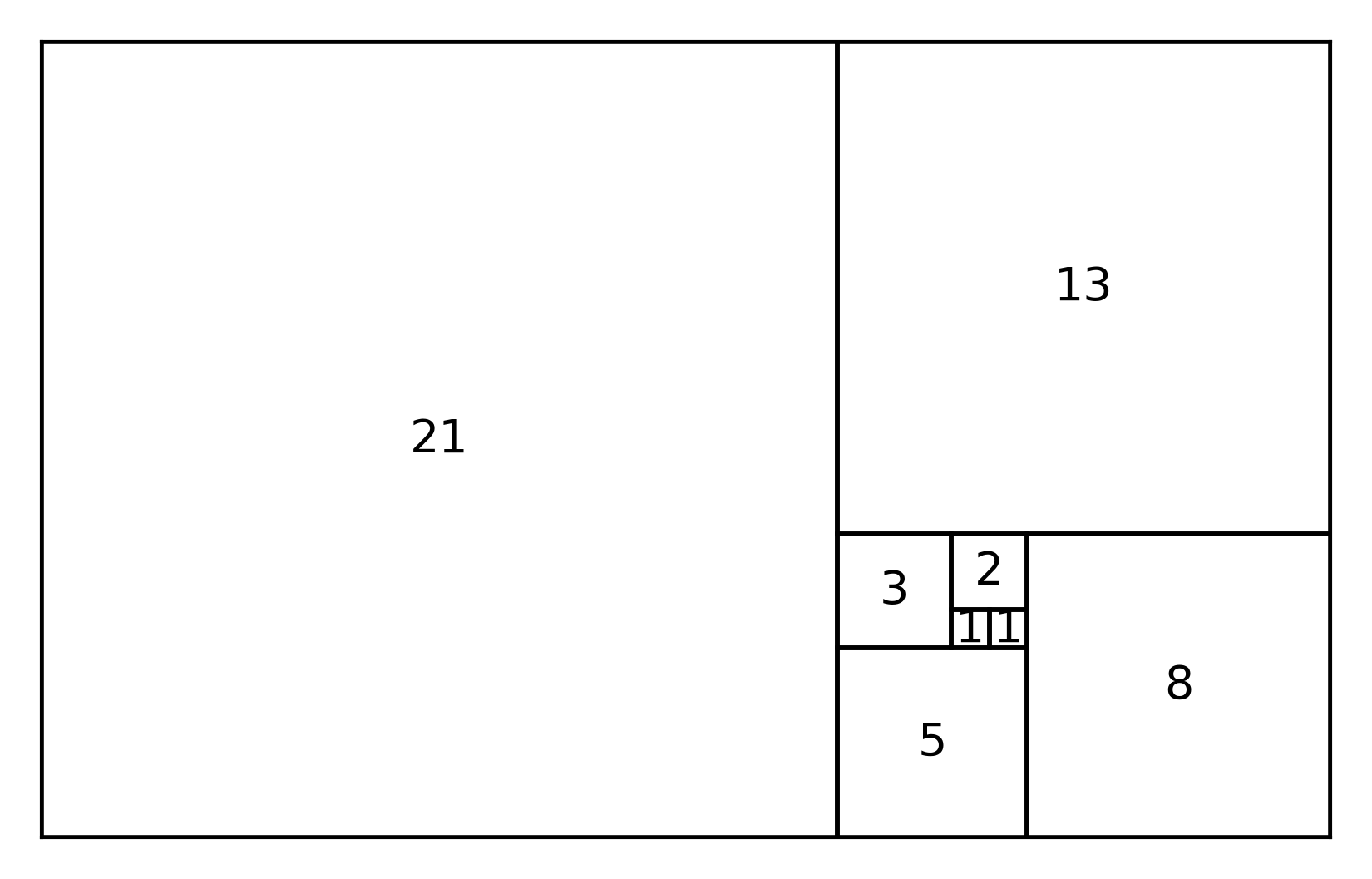
La razón entre los números de Fibonacci
Si se toma la razón entre dos números de Fibonacci consecutivos, el resultado se aproxima a una constante llamada la proporción áurea \(\phi\):
$$ \phi = \frac{1+\sqrt{5}}{2} \approx 1,618... $$
Ejemplo: $$ \frac{55}{34} \approx 1,6176 $$ Cuanto mayores son los números, más se aproxima a \(\phi\).
Fórmula de Binet
Existe una fórmula explícita (llamada fórmula de Binet) que permite calcular un número de Fibonacci sin conocer los anteriores:
$$ F_n = \frac{1}{\sqrt{5}}\Biggl(\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Biggr) $$
Con la fórmula de Binet podemos calcular:
$$ F_{25} = 75025 $$
El 25º número de Fibonacci es por lo tanto 75025.
La espiral de Fibonacci
Al dibujar los cuadrados de Fibonacci, se puede trazar una espiral desde el centro hacia fuera. Esta espiral se encuentra en muchos patrones naturales: semillas de girasol, conchas, coliflor.

Hay muchos lugares donde vemos y usamos los números de Fibonacci y la espiral en la vida cotidiana:
- Naturaleza – crecimiento de plantas, patrones de flores, semillas y conchas.
- Arte y arquitectura – proporciones y composiciones basadas en Fibonacci y la proporción áurea.
- Informática – algoritmos, estructuras de datos (Fibonacci heap) y búsqueda eficiente.
- Música – algunos compositores han usado los números de Fibonacci para estructurar ritmos y compases.
Patrones en los números de Fibonacci
La suma de los primeros \(n\) números de Fibonacci:
La suma es siempre uno menos que el \((n+2)\)-ésimo número de Fibonacci:
$$ F_1 + F_2 + \cdots + F_n = F_{n+2} - 1 $$
Ejemplo:
Los primeros 5 números de Fibonacci son \(1,1,2,3,5\). La suma es:
$$ 1+1+2+3+5 = 12 $$
El 7º número de Fibonacci es 13, y \(13-1=12\). La regla se cumple.
La suma de los cuadrados de los números de Fibonacci:
La suma de los cuadrados hasta \(F_n\) es igual al producto de \(F_n\) y \(F_{n+1}\):
$$ F_1^2 + F_2^2 + \cdots + F_n^2 = F_n \cdot F_{n+1} $$
Ejemplo 1:
Para \(n=3\):
$$ 1^2+1^2+2^2+3^2 = 15 $$
Y al mismo tiempo:
$$ 3 \cdot 5 = 15 $$
Ejemplo 2:
Para \(n=5\):
$$ 1^2+1^2+2^2+3^2+5^2 = 40 $$
Y:
$$ 5 \cdot 8 = 40 $$
La regla se cumple para todos los números de Fibonacci.
Otros patrones:
- Cada segundo número de Fibonacci es par.
- Cada tercero es divisible por 2, cada cuarto por 3, etc.
- Los números de Fibonacci se pueden encontrar como sumas diagonales en el triángulo de Pascal.
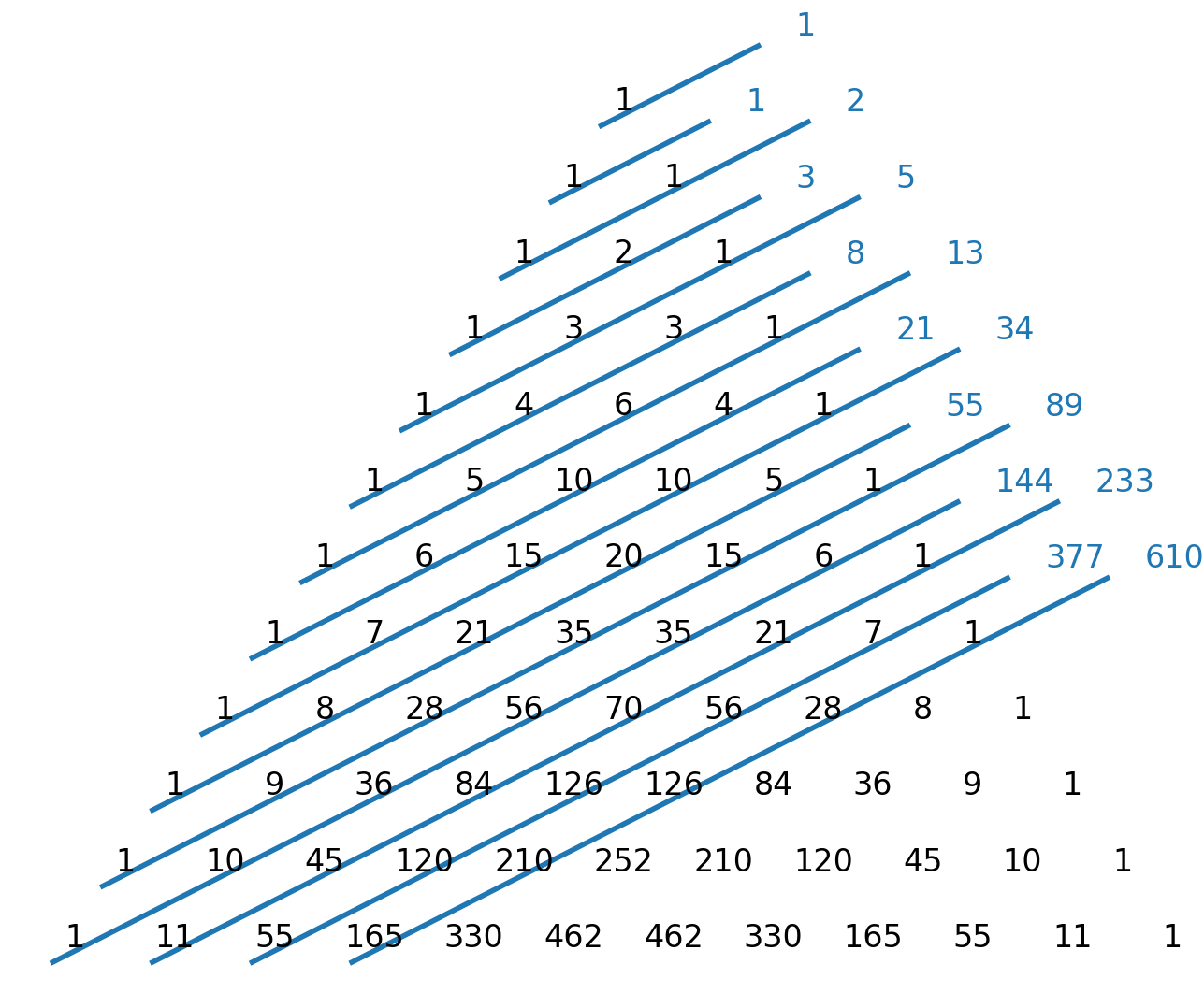
Resumen
La sucesión de Fibonacci comienza de forma simple: \(0, 1, 1, 2, 3, 5...\), pero contiene patrones profundos y conexiones con la naturaleza, el arte y las matemáticas.
Desde definiciones recursivas hasta la fórmula de Binet y la proporción áurea, los números de Fibonacci son a la vez bellos y prácticos.