Números

Los Números son un concepto amplio, usado fundamentalmente para indicar una Cantidad o un Tamaño.

Existen muchos Tipos diferentes de Números, que se dividen en Categorías. En Matemáticas trabajamos con todos ellos, y se pueden ver como Conjuntos anidados, donde cada nueva Categoría amplía la anterior.

A continuación se ofrece una breve descripción de las Categorías más importantes.

 

Números Naturales \(\ N\)

Los Números Naturales son todos los Números enteros mayores que cero: 1, 2, 3, 4, 5, 6 … etc. Se denotan con \(\large N\). En algunos contextos, también se incluye el 0, y entonces se escribe \(\large N_0\).

 

Números Enteros \(\ Z\)

Si ampliamos los Números Naturales (incluido el 0) con los Números negativos, obtenemos los Números Enteros:

… -4, -3, -2, -1, 0, 1, 2, 3 … etc.

Se denotan con \(\large Z\).

 

Números Racionales \(\ Q\)

Los Números Racionales son todos los Números que se pueden escribir como una Fracción, donde el Numerador es un Número Entero y el Denominador un Número Natural distinto de 0. Ejemplos:

 

\(\large \frac{1}{4} = 0,25\), \(\large -\frac{3}{5} = -0,6\)

 

También pertenecen aquí todas las Fracciones Decimales finitas y periódicas.

Se denotan con \(\large Q\).

 

Números Reales \(\ R\)

Los Números Reales incluyen todos los Conjuntos de Números mencionados anteriormente, pero también los Números Irracionales, que no se pueden escribir como Fracciones. Los Números Irracionales tienen un desarrollo Decimal infinito no periódico.

 

Ejemplos son \(\large \pi\) y \(\large \sqrt{5}\).

 

\(\large \sqrt{5} \) es un Número Real, pero al mismo tiempo un Número Irracional, porque no se puede escribir como una Fracción.

Los Números Reales se denotan con \(\large R\).

 

Números Complejos \(\ C\)

Los Números Complejos amplían los Números Reales al incluir los Números Imaginarios. Mientras que un Número Real se puede colocar en una Recta Numérica, un Número Complejo se puede representar en el Plano como un Punto con las Coordenadas \(\large (x,y)\), donde \(x\) es la Parte Real, y \(\large y\) es la Parte Imaginaria. Un Número Complejo se escribe en la forma:

 

\(\large z = x + yi \)

 

Aquí \(i\) es la Unidad Imaginaria, definida por \(\large i^2 = -1\). Un ejemplo es:

 

\(\large z = 3 + 2i \)

 

Se puede entender como el Punto \(\large (3,2)\) en el Plano Complejo.

Los Números Complejos se usan, por ejemplo, para resolver Ecuaciones que no tienen Soluciones Reales, como:

 

\(\large x^2 + 1 = 0 \implies x = \pm i \)

 

Los Números Complejos se denotan con \(\large C\).

 

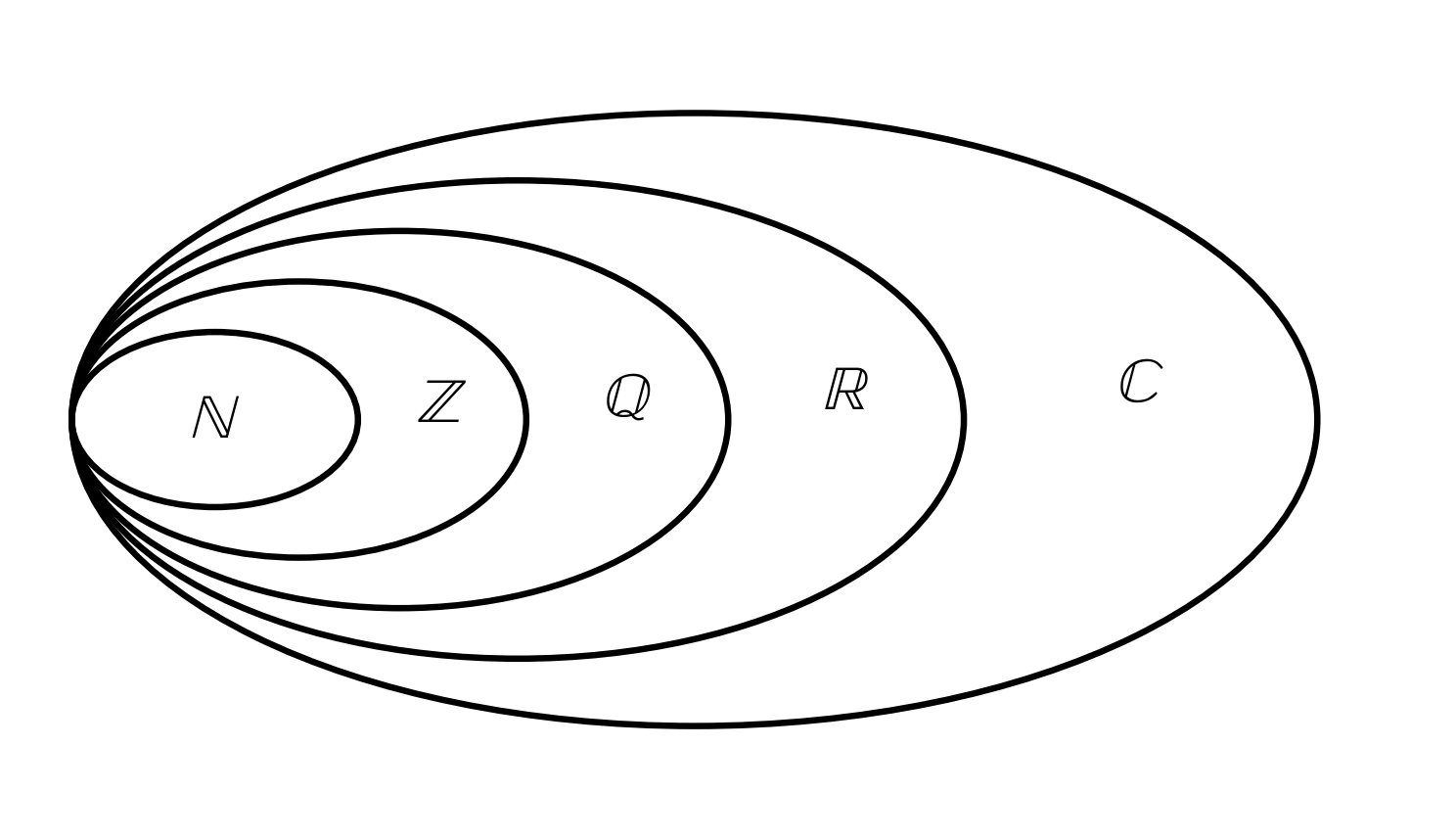
La Imagen muestra los Números Naturales como parte de los Números Enteros, que a su vez forman parte de los Números Racionales, etc.

 

Resumen

La Jerarquía entre los Conjuntos Numéricos se puede escribir brevemente así:

 

\(\Large N \subset Z \subset Q \subset R \subset C\)