Números cuadrados

Un Número Cuadrado es el resultado de elevar un Número al cuadrado.

En otras palabras, un Número Cuadrado tiene la forma \(\large n^2\), donde \(n\) es un Número Natural.

 

Ejemplo

\(\large 3^2 = 9,\quad 6^2 = 36,\quad 10^2 = 100\)

 

Si tomas la Raíz Cuadrada de \(X\) y el resultado es un Número Entero, entonces \(X\) es un Número Cuadrado. Por ejemplo, \(\large \sqrt{81} = 9\), así que 81 es un Número Cuadrado.

 

Significado geométrico

Un Número Cuadrado puede verse como el área de un Cuadrado con lado \(n\). Por ejemplo, 16 es el área de un Cuadrado con lado 4.

 

\(\large \sqrt{16} = 4\)

 

Parábola en el sistema de coordenadas

Los puntos \((n, n^2)\) forman la gráfica de la función \(\large y = x^2\), que es una Parábola.

 

 

 

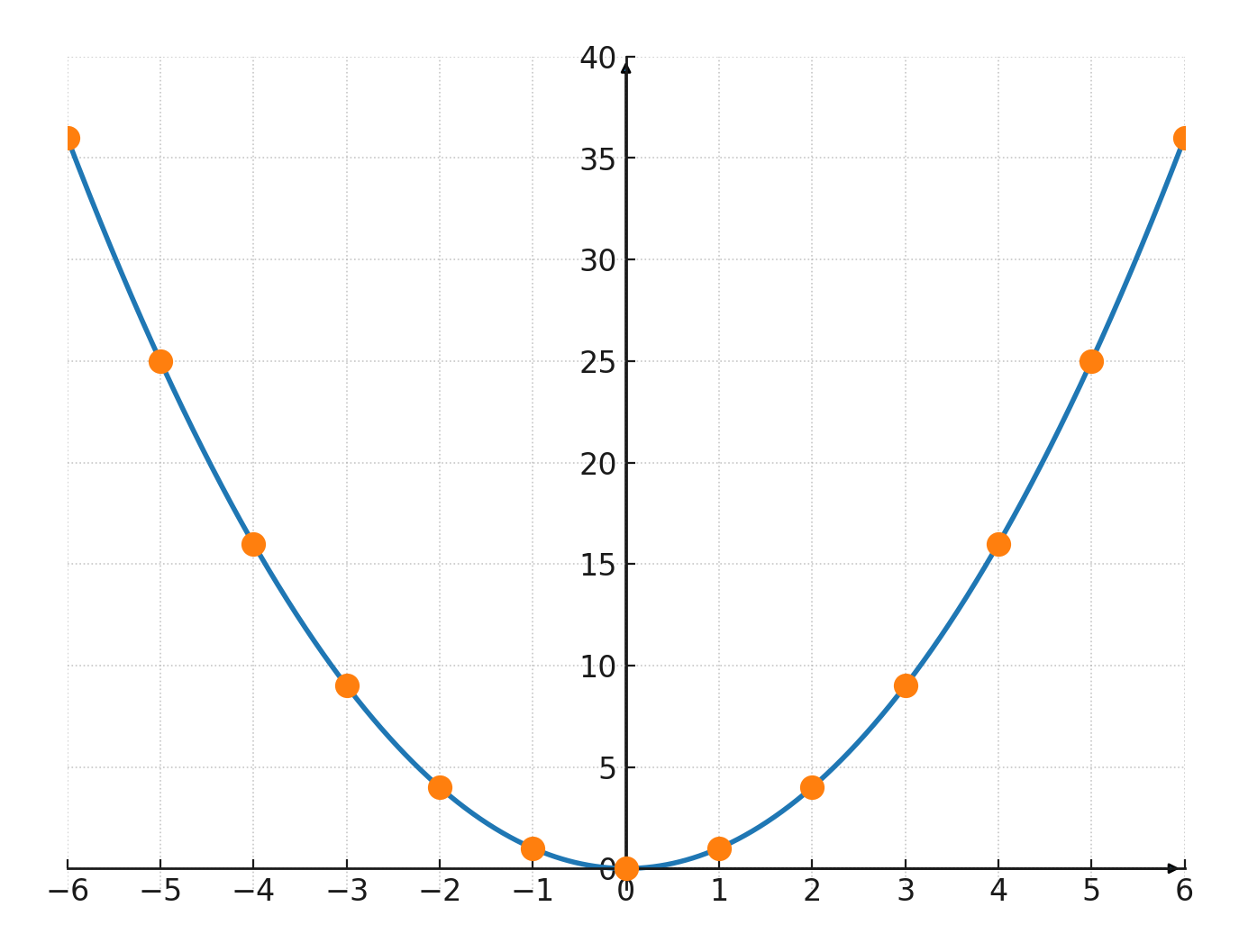
Tabla de los primeros Números Cuadrados

 

Número (raíz)	1	2	3	4	5	6	7	8	9	10
Número Cuadrado	1	4	9	16	25	36	49	64	81	100

 

 

Patrones en Números Cuadrados

Diferencia entre dos Números Cuadrados consecutivos:

 

\(\large (n+1)^2 - n^2 = 2n + 1\). La diferencia es siempre un Número Impar.

 

Suma de los primeros \(n\) Números Impares:

 

\(\large 1 + 3 + 5 + \cdots + (2n-1) = n^2\). Por ejemplo \(\large 1+3+5+7+9 = 25\).

 

Última cifra:

 

Un Número Cuadrado solo puede terminar en 0, 1, 4, 5, 6 o 9.

 

Módulo 3:

 

Un Número Cuadrado es divisible por 3 o uno más que un múltiplo de 3.

 

 

Números Cuadrados y Factores Primos

Un Número es un Número Cuadrado si y solo si todos los exponentes en su Factorización Prima son Pares.

 

Por ejemplo \(\large 900 = 2^2 \cdot 3^2 \cdot 5^2 = (2\cdot 3\cdot 5)^2\).

 

 

Conexiones con otros temas

Pitágoras:

 

Los Números Cuadrados aparecen en el Teorema de Pitágoras \(\large a^2 + b^2 = c^2\). Un ejemplo clásico es \(\large 3^2 + 4^2 = 5^2\).

 

Diferencia de Cuadrados:

 

\(\large a^2 - b^2 = (a-b)(a+b)\).