Kvadrattal

Et Kvadrattal er resultatet af at opløfte et Tal i anden potens.

Med andre ord er et Kvadrattal på formen \(\large n^2\), hvor \(n\) er et Naturligt Tal.

 

Eksempel

\(\large 3^2 = 9,\quad 6^2 = 36,\quad 10^2 = 100\)

 

Hvis du tager Kvadratroden af \(X\) og resultatet er et Heltal, så er \(X\) et Kvadrattal. For eksempel er \(\large \sqrt{81} = 9\), så 81 er et Kvadrattal.

 

Geometrisk betydning

Et Kvadrattal kan ses som arealet af et Kvadrat med sidelængde \(n\). For eksempel er 16 arealet af et Kvadrat med sidelængde 4.

 

\(\large \sqrt{16} = 4\)

 

Parabel i koordinatsystemet

Punkterne \((n, n^2)\) danner grafen for funktionen \(\large y = x^2\), som er en Parabel.

 

 

 

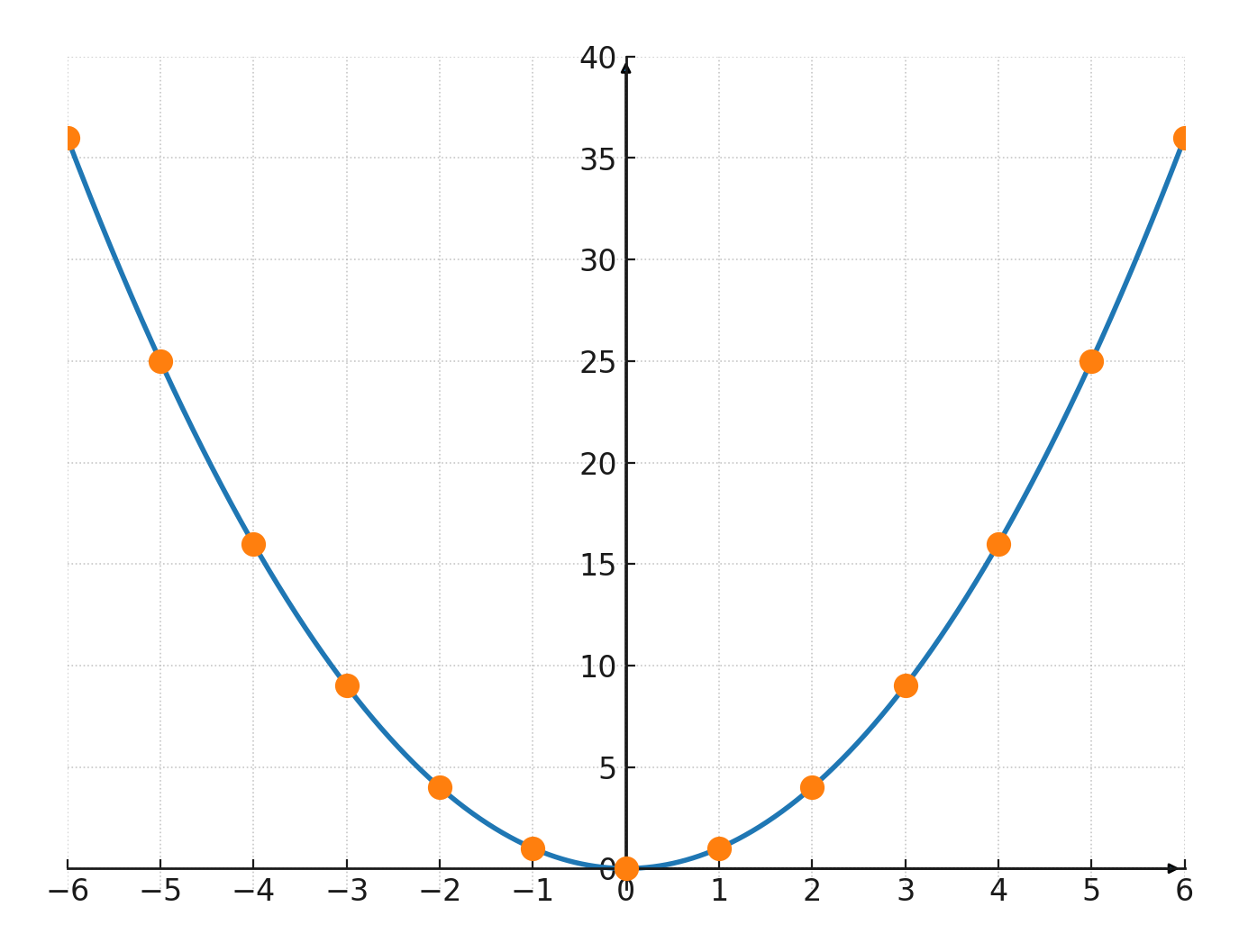
Tabel over de første Kvadrattal

 

Nummer (rod)	1	2	3	4	5	6	7	8	9	10
Kvadrattal	1	4	9	16	25	36	49	64	81	100

 

 

Mønstre i Kvadrattal

Forskel mellem to på hinanden følgende Kvadrattal:

 

\(\large (n+1)^2 - n^2 = 2n + 1\). Forskellen er altid et ulige Tal.

 

Sum af de første \(n\) ulige Tal:

 

\(\large 1 + 3 + 5 + \cdots + (2n-1) = n^2\). For eksempel \(\large 1+3+5+7+9 = 25\).

 

Sidste ciffer:

 

Et Kvadrattal kan kun slutte på 0, 1, 4, 5, 6 eller 9.

 

Modulus 3:

 

Et Kvadrattal er enten deleligt med 3 eller én mere end et multiplum af 3. Det vil sige \(\large n^2 \equiv 0\) eller \(\large 1 \pmod{3}\).

 

 

Kvadrattal og Primfaktorer

Et Tal er et Kvadrattal hvis og kun hvis alle eksponenter i dets Primfaktorisering er lige Tal.

 

For eksempel er \(\large 900 = 2^2 \cdot 3^2 \cdot 5^2 = (2\cdot 3\cdot 5)^2\), altså et Kvadrattal.

 

 

Forbindelser til andre emner

Pythagoras:

 

Kvadrattal optræder i Pythagoras Sætning \(\large a^2 + b^2 = c^2\). Et klassisk eksempel er \(\large 3^2 + 4^2 = 5^2\), altså \(\large 9 + 16 = 25\).

 

Forskel af Kvadrater:

 

 \(\large a^2 - b^2 = (a-b)(a+b)\) bruges ofte ved omskrivninger og faktorisering.