Tal

Tal er et bredt begreb, der grundlæggende bruges til at angive en Mængde eller en Størrelse.

Der findes mange forskellige Typer Tal, som er inddelt i Kategorier. I Matematikken arbejder vi med dem alle, og de kan ses som indlejrede Mængder, hvor hver ny Kategori udvider den forrige.

Nedenfor følger en kort beskrivelse af de vigtigste Kategorier.

 

Naturlige Tal \(\ N\)

De Naturlige Tal er alle hele Tal større end nul: 1, 2, 3, 4, 5, 6 … osv. De betegnes med \(\large N\).

I nogle sammenhænge vælger man også at medtage 0, og så skriver man \(\large N_0\).

 

Heltal \(\ Z\)

Udvider vi de Naturlige Tal (inklusive 0) med de negative Tal, får vi Heltallene:

… -4, -3, -2, -1, 0, 1, 2, 3 … osv.

De betegnes med \(\large Z\).

 

Rationale Tal \(\ Q\)

De Rationale Tal er alle Tal, der kan skrives som en Brøk, hvor Tælleren er et Heltal og Nævneren et Naturligt Tal forskelligt fra 0. Eksempler:

 

\(\large \frac{1}{4} = 0,25\), \(\large -\frac{3}{5} = -0,6\)

 

Alle endelige og periodiske Decimalbrøker hører også til her.

De betegnes med \(\large Q\).

 

Reelle Tal \(\ R\)

De Reelle Tal omfatter alle de tidligere nævnte Talmængder, men også de Irrationale Tal, som ikke kan skrives som Brøker. Irrationale Tal har en uendelig ikke-periodisk Decimaludvikling.

 

Eksempler er \(\large \pi\) og \(\large \sqrt{5}\).

 

\(\large \sqrt{5} \) er et Reelt Tal, men samtidigt et Irrationalt Tal, fordi det ikke kan skrives som en Brøk.

De Reelle Tal betegnes med \(\large R\).

 

Komplekse Tal \(\ C\)

De Komplekse Tal udvider de Reelle Tal ved at inkludere de Imaginære Tal. Hvor et Reelt Tal kan placeres på en Tallinje, kan et Komplekst Tal repræsenteres i Planen som et Punkt med Koordinaterne \(\large (x,y)\), hvor \(x\) er den Reelle Del, og \(\large y\) er den Imaginære Del. Et Komplekst Tal skrives på formen:

 

\(\large z = x + yi \)

 

Her er \(i\) den Imaginære Enhed, defineret ved at \(\large i^2 = -1\). Et eksempel er:

 

\(\large z = 3 + 2i \)

 

Det kan forstås som Punktet \(\large (3,2)\) i det Komplekse Plan.

 

Komplekse Tal bruges bl.a. til at løse Ligninger, der ikke har nogen Reelle Løsninger, fx:

 

\(\large x^2 + 1 = 0 \implies x = \pm i \)

 

De Komplekse Tal betegnes med \(\large C\).

 

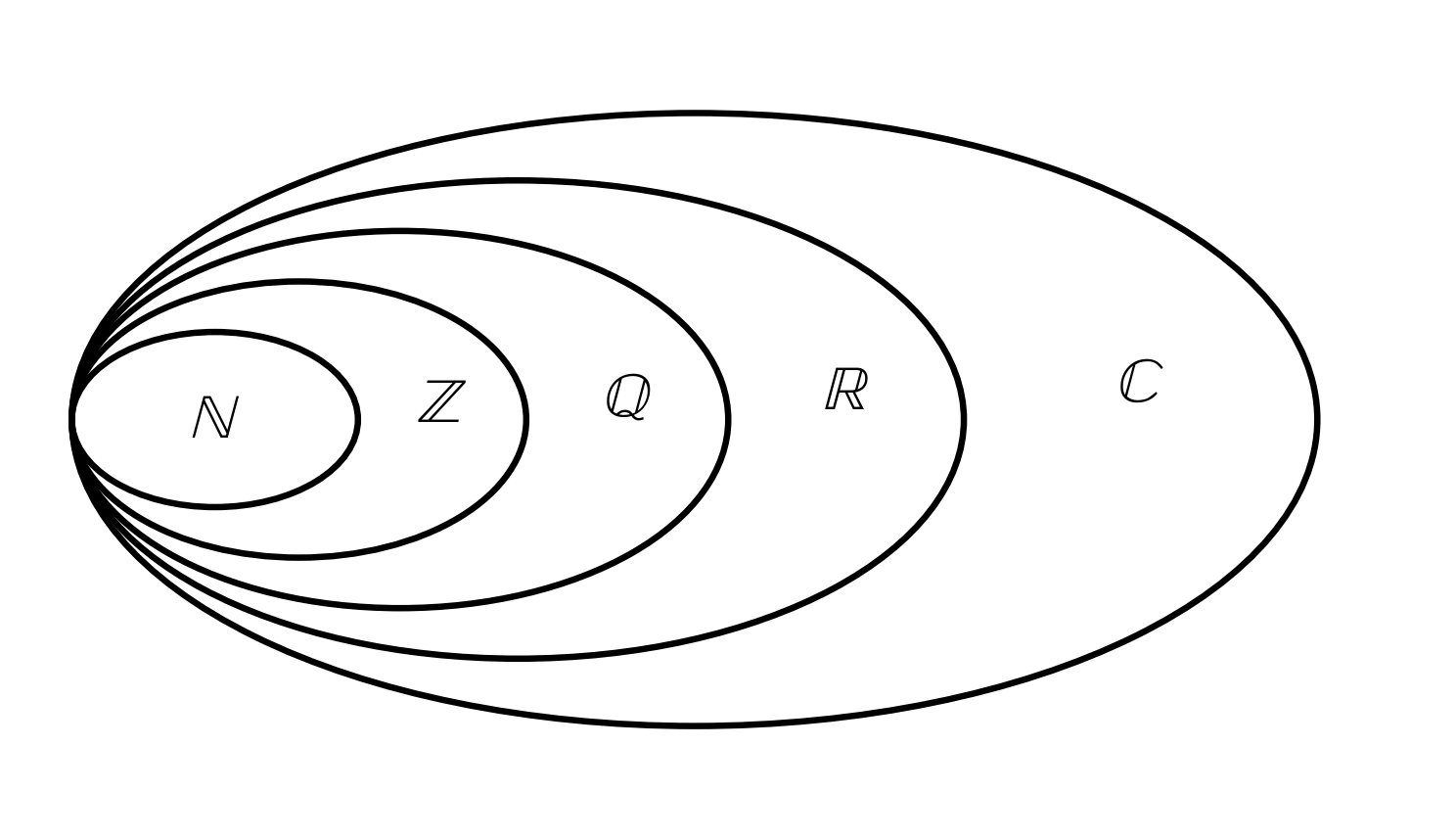
Billedet viser de Naturlige Tal som en del af Heltallene, der igen er en del af de Rationale Tal osv.

 

Opsummering

Hierarkiet mellem Talmængderne kan skrives kort sådan:

 

\(\Large N \subset Z \subset Q \subset R \subset C\)