Fibonacci tal

Fibonacci-tal er opkaldt efter Leonardo Fibonacci, en italiensk matematiker, som beskrev denne talrække første gang i år 1202 i bogen Liber Abaci.

 

Rekursiv definition

Fibonacci-tallene defineres ved en rekursiv funktion:

 

$$ F_0 = 0, \quad F_1 = 1 $$

$$ F_n = F_{n-1} + F_{n-2} \quad (n \geq 2) $$

 

Det betyder, at hvert tal i rækken er summen af de to foregående.

De første 10 Fibonacci-tal er derfor:

 

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 $$

 

Man ser hurtigt mønsteret:

 

$$ 0+1=1,\;\;1+1=2,\;\;1+2=3,\;\;2+3=5,\;\;3+5=8\;\;osv. $$

 

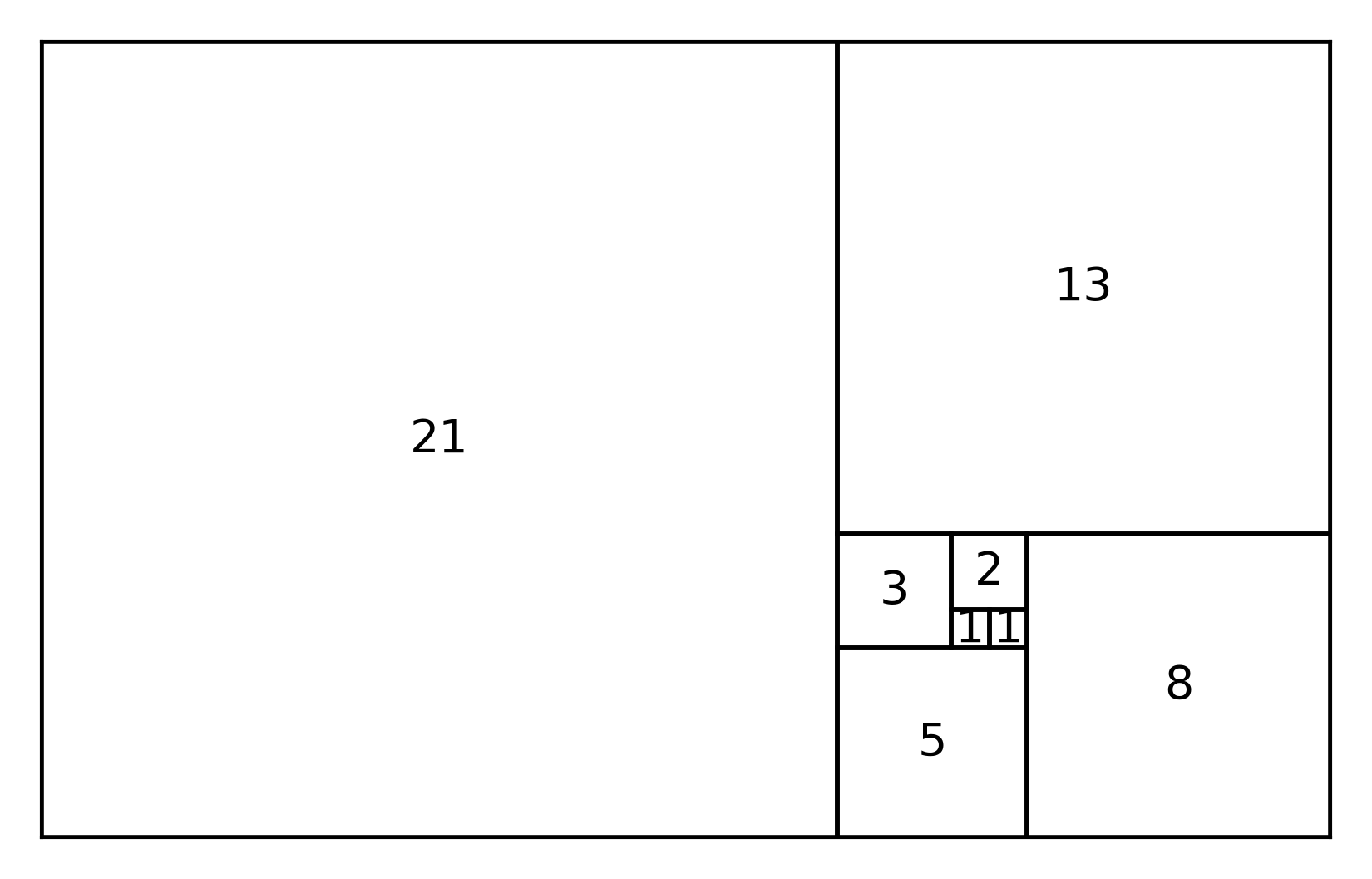
Fibonacci-tal kan illustreres ved kvadrater med sidelængde lig tallene. 

 

 

 

Forholdet mellem Fibonacci-tal

Hvis man tager forholdet mellem to på hinanden følgende Fibonacci-tal, nærmer resultatet sig en bestemt konstant kaldet det gyldne snit \(\phi\):

 

$$ \phi = \frac{1+\sqrt{5}}{2} \approx 1,618... $$

 

Eksempel: $$ \frac{55}{34} \approx 1,6176 $$ Jo større tallene er, desto tættere kommer man på \(\phi\).

 

 

Binet’s formel

Der findes en eksplicit formel (kaldet Binet’s formel), som gør det muligt at beregne et Fibonacci-tal uden at kende de foregående:

 

$$ F_n = \frac{1}{\sqrt{5}}\Biggl(\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Biggr) $$

 

Ved hjælp af Binet’s formel kan vi beregne:

 

$$ F_{25} = 75025 $$

 

Det 25. Fibonacci-tal er altså 75025.

 

 

Fibonacci-spiralen

Når man tegner Fibonacci-kvadraterne, kan der tegnes en spiral fra midten og ud. Denne spiral findes i mange naturlige mønstre: solsikkens frø, sneglehuse, blomkål.

 

 

Der er mange steder vi ser og bruger Fibonacci tallene og spiralen i hverdagen:

 

• Naturen – planters vækst, blomsters mønstre, frø og skaller.
• Kunst og arkitektur – proportioner og kompositioner baseret på Fibonacci og det gyldne snit.
• Datalogi – algoritmer, datastrukturer (Fibonacci-heap) og effektiv søgning.
• Musik – nogle komponister har brugt Fibonacci-tal til at strukturere rytmer og takter.

 

 

Mønstre i Fibonacci-tal

Summen af de første \(n\) Fibonacci-tal:

 

Summen er altid ét mindre end det \((n+2)\)-te Fibonacci-tal:

$$ F_1 + F_2 + \cdots + F_n = F_{n+2} - 1 $$

 

Eksempel:

De første 5 Fibonacci-tal er \(1,1,2,3,5\). Summen er:

$$ 1+1+2+3+5 = 12 $$

Det 7. Fibonacci-tal er 13, og \(13-1=12\). Reglen passer.

 

Summen af Fibonacci-tallenes kvadrater:

 

Summen af kvadraterne op til \(F_n\) er lig med produktet af \(F_n\) og \(F_{n+1}\):

$$ F_1^2 + F_2^2 + \cdots + F_n^2 = F_n \cdot F_{n+1} $$

 

Eksempel 1:

For \(n=3\):

$$ 1^2+1^2+2^2+3^2 = 15 $$

Og samtidig:

$$ 3 \cdot 5 = 15 $$

 

Eksempel 2:

For \(n=5\):

$$ 1^2+1^2+2^2+3^2+5^2 = 40 $$

Og:

$$ 5 \cdot 8 = 40 $$

 

Reglen gælder for alle Fibonacci-tal.

 

Andre mønstre:

• Hvert andet Fibonacci-tal er lige.
• Hvert tredje er deleligt med 2, hvert fjerde med 3 osv.
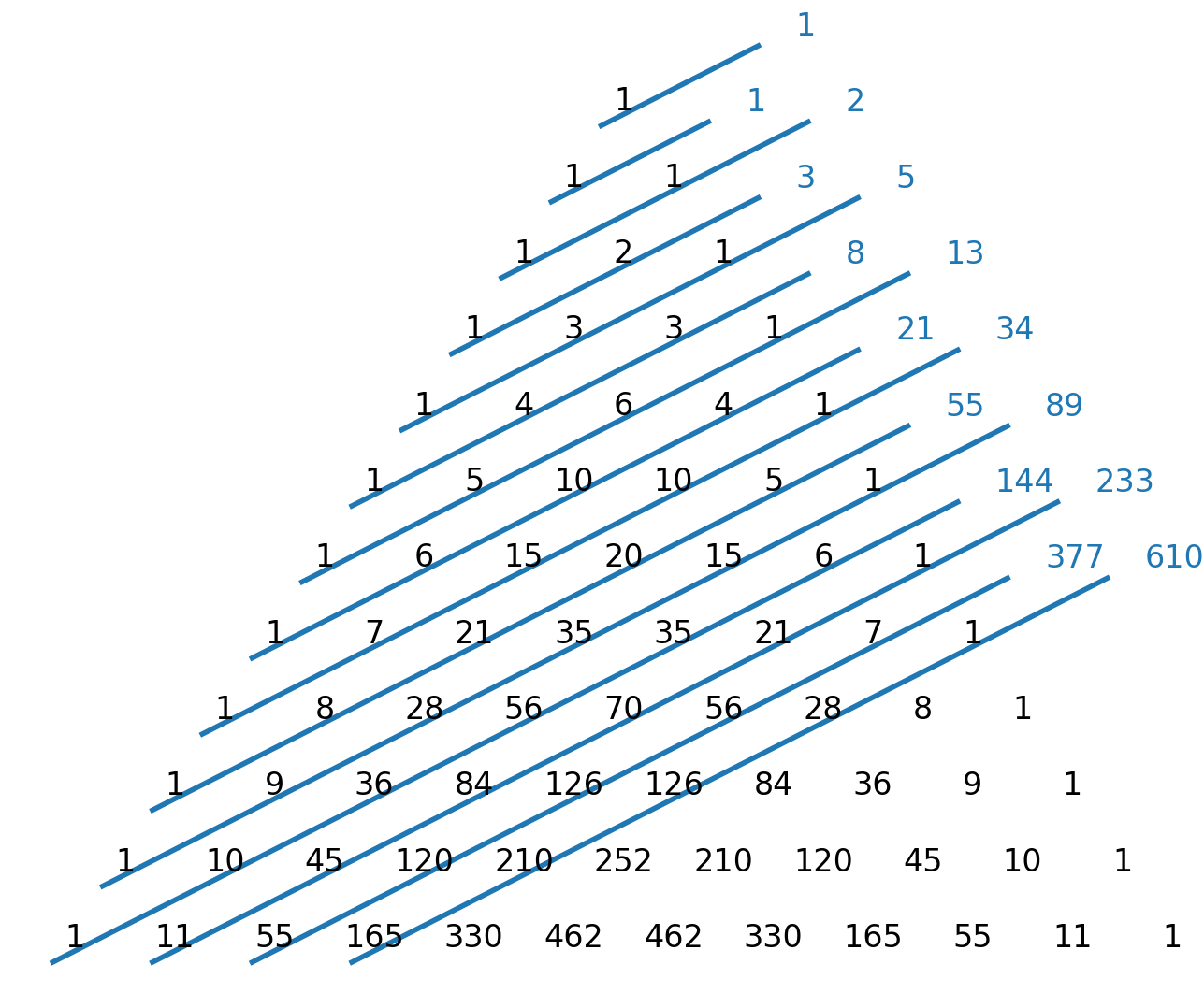
• Fibonacci-tallene kan findes som diagonalsummer i Pascals trekant.

 

 

Opsummering

Fibonacci-rækken starter simpelt: \(0, 1, 1, 2, 3, 5...\), men den indeholder dybe mønstre og forbindelser til natur, kunst og matematik.

Fra rekursive definitioner til Binet’s formel og det gyldne snit, Fibonacci-tal er både smukke og praktiske.