Nombres de Fibonacci
Les nombres de Fibonacci portent le nom de Leonardo Fibonacci, un mathématicien italien, qui a décrit cette suite pour la première fois en 1202 dans le livre Liber Abaci.
Définition récursive
Les nombres de Fibonacci sont définis par une fonction récursive :
$$ F_0 = 0, \quad F_1 = 1 $$
$$ F_n = F_{n-1} + F_{n-2} \quad (n \geq 2) $$
Cela signifie que chaque nombre de la suite est la somme des deux précédents.
Les 10 premiers nombres de Fibonacci sont donc :
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 $$
On remarque rapidement le schéma :
$$ 0+1=1,\;\;1+1=2,\;\;1+2=3,\;\;2+3=5,\;\;3+5=8\;\;etc. $$
Les nombres de Fibonacci peuvent être illustrés par des carrés dont la longueur du côté correspond aux nombres.
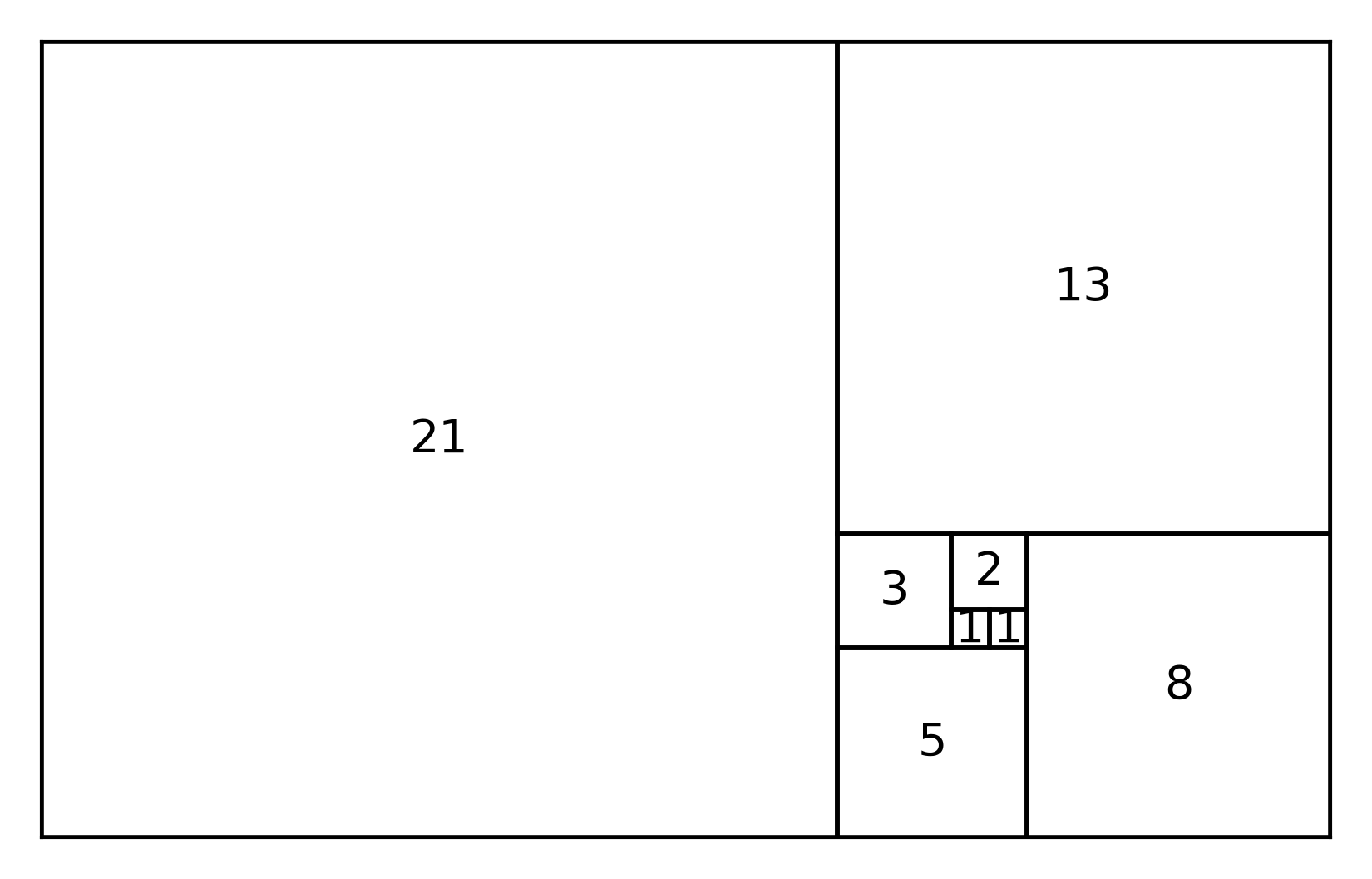
Le rapport entre les nombres de Fibonacci
Si l’on prend le rapport entre deux nombres de Fibonacci consécutifs, le résultat se rapproche d’une constante appelée le nombre d’or \(\phi\) :
$$ \phi = \frac{1+\sqrt{5}}{2} \approx 1,618... $$
Exemple : $$ \frac{55}{34} \approx 1,6176 $$ Plus les nombres sont grands, plus on se rapproche de \(\phi\).
Formule de Binet
Il existe une formule explicite (appelée formule de Binet) qui permet de calculer un nombre de Fibonacci sans connaître les précédents :
$$ F_n = \frac{1}{\sqrt{5}}\Biggl(\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Biggr) $$
Avec la formule de Binet, on peut calculer :
$$ F_{25} = 75025 $$
Le 25e nombre de Fibonacci est donc 75025.
La spirale de Fibonacci
En traçant les carrés de Fibonacci, on peut dessiner une spirale du centre vers l’extérieur. Cette spirale se retrouve dans de nombreux motifs naturels : graines de tournesol, coquillages, chou-fleur.

Il existe de nombreux endroits où l’on voit et utilise les nombres de Fibonacci et la spirale dans la vie quotidienne :
- Nature – croissance des plantes, motifs des fleurs, graines et coquilles.
- Art et architecture – proportions et compositions basées sur Fibonacci et le nombre d’or.
- Informatique – algorithmes, structures de données (tas de Fibonacci) et recherche efficace.
- Musique – certains compositeurs ont utilisé les nombres de Fibonacci pour structurer rythmes et mesures.
Motifs dans les nombres de Fibonacci
La somme des \(n\) premiers nombres de Fibonacci :
La somme est toujours égale à un de moins que le \((n+2)\)-ième nombre de Fibonacci :
$$ F_1 + F_2 + \cdots + F_n = F_{n+2} - 1 $$
Exemple :
Les 5 premiers nombres de Fibonacci sont \(1,1,2,3,5\). La somme est :
$$ 1+1+2+3+5 = 12 $$
Le 7e nombre de Fibonacci est 13, et \(13-1=12\). La règle est vérifiée.
La somme des carrés des nombres de Fibonacci :
La somme des carrés jusqu’à \(F_n\) est égale au produit de \(F_n\) et \(F_{n+1}\) :
$$ F_1^2 + F_2^2 + \cdots + F_n^2 = F_n \cdot F_{n+1} $$
Exemple 1 :
Pour \(n=3\) :
$$ 1^2+1^2+2^2+3^2 = 15 $$
Et en même temps :
$$ 3 \cdot 5 = 15 $$
Exemple 2 :
Pour \(n=5\) :
$$ 1^2+1^2+2^2+3^2+5^2 = 40 $$
Et :
$$ 5 \cdot 8 = 40 $$
La règle est valable pour tous les nombres de Fibonacci.
Autres motifs :
- Un nombre de Fibonacci sur deux est pair.
- Chaque troisième est divisible par 2, chaque quatrième par 3, etc.
- Les nombres de Fibonacci peuvent être trouvés comme sommes diagonales dans le triangle de Pascal.
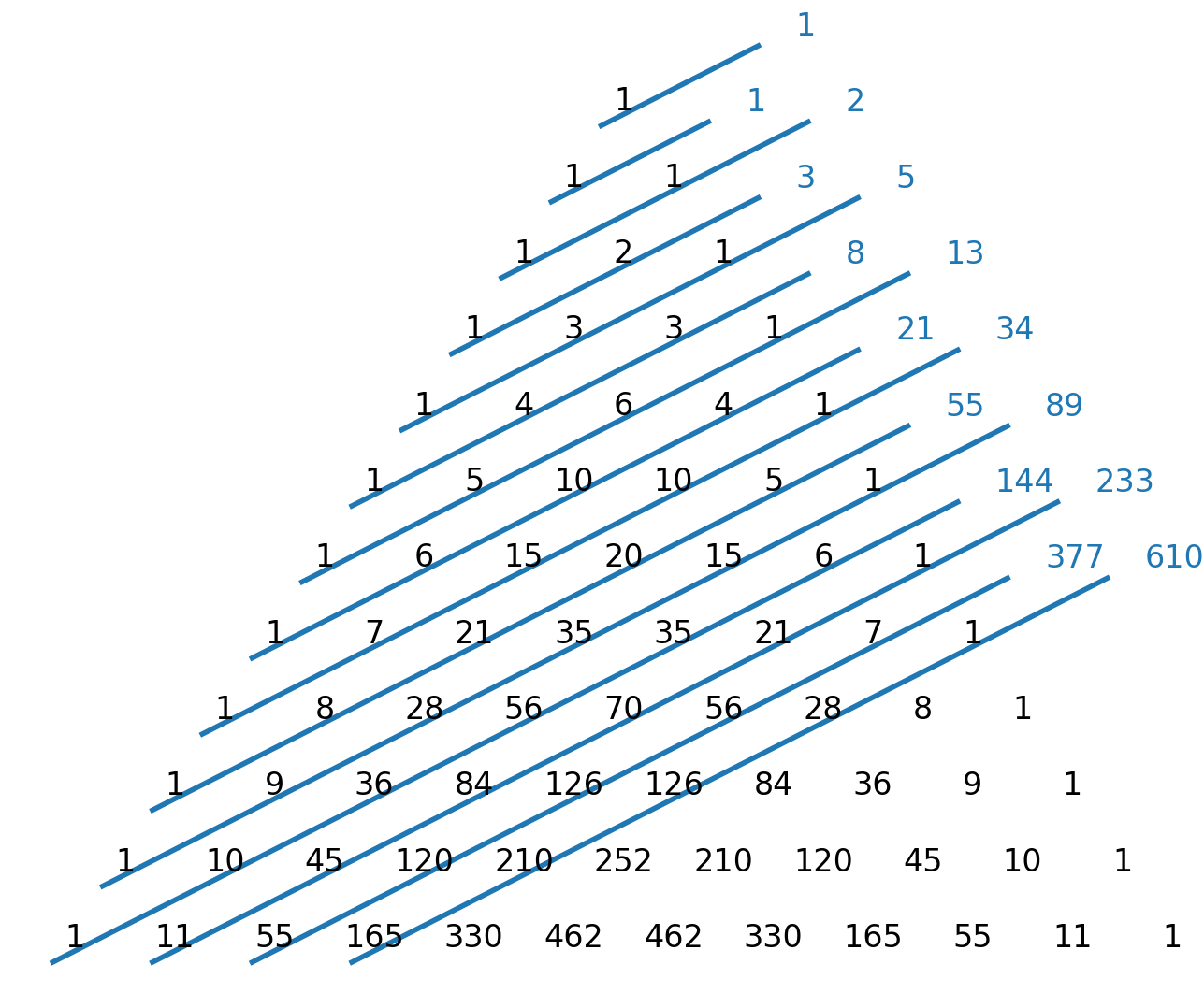
Résumé
La suite de Fibonacci commence simplement : \(0, 1, 1, 2, 3, 5...\), mais elle contient des motifs profonds et des liens avec la nature, l’art et les mathématiques.
Des définitions récursives à la formule de Binet et au nombre d’or, les nombres de Fibonacci sont à la fois beaux et utiles.