Nombres carrés

Un Nombre Carré est le résultat d’élever un Nombre au carré.

En d’autres termes, un Nombre Carré a la forme \(\large n^2\), où \(n\) est un Nombre Naturel.

 

Exemple

\(\large 3^2 = 9,\quad 6^2 = 36,\quad 10^2 = 100\)

 

Si vous prenez la Racine Carrée de \(X\) et que le résultat est un Nombre Entier, alors \(X\) est un Nombre Carré. Par exemple, \(\large \sqrt{81} = 9\).

 

Signification géométrique

Un Nombre Carré peut être vu comme l’aire d’un Carré de côté \(n\). Par exemple, 16 est l’aire d’un Carré de côté 4.

 

\(\large \sqrt{16} = 4\)

 

Parabole dans le système de coordonnées

Les points \((n, n^2)\) forment la courbe de la fonction \(\large y = x^2\), qui est une Parabole.

 

 

 

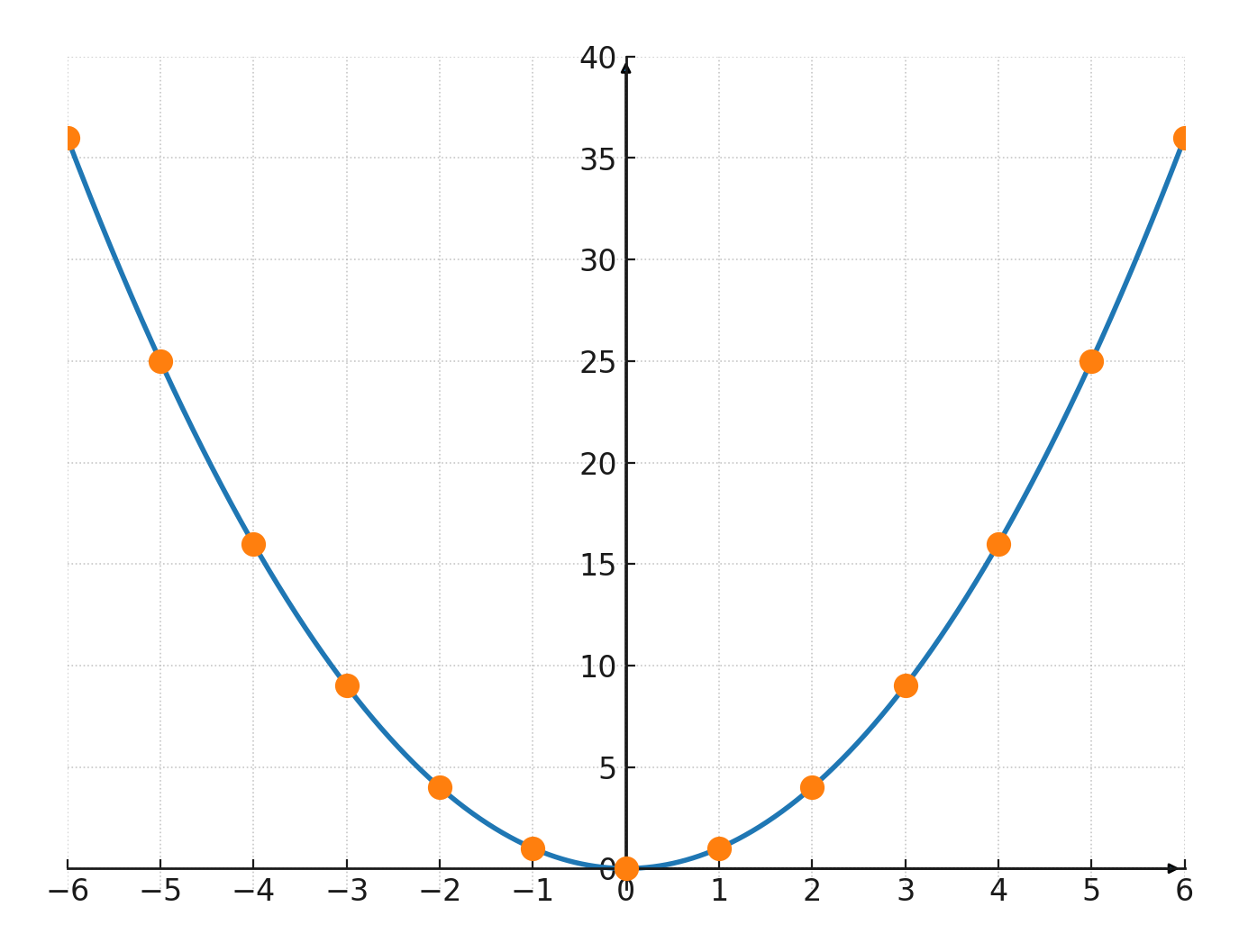
Table des premiers Nombres Carrés

 

Nombre (racine)	1	2	3	4	5	6	7	8	9	10
Nombre Carré	1	4	9	16	25	36	49	64	81	100

 

 

Motifs dans les Nombres Carrés

Différence entre deux Nombres Carrés consécutifs :

 

\(\large (n+1)^2 - n^2 = 2n + 1\). La différence est toujours un Nombre Impair.

 

Somme des \(n\) premiers Nombres Impairs :

 

\(\large 1 + 3 + 5 + \cdots + (2n-1) = n^2\). Par exemple \(\large 1+3+5+7+9 = 25\).

 

Dernier chiffre :

 

Un Nombre Carré se termine toujours par 0, 1, 4, 5, 6 ou 9.

 

Modulo 3 :

 

Un Nombre Carré est soit divisible par 3 soit égal à 1 de plus qu’un multiple de 3.

 

 

Nombres Carrés et Facteurs Premiers

Un Nombre est un Nombre Carré si et seulement si tous les exposants de sa Factorisation Première sont Pairs.

 

Par exemple \(\large 900 = 2^2 \cdot 3^2 \cdot 5^2 = (2\cdot 3\cdot 5)^2\).

 

 

Liens avec d’autres thèmes

Pythagore :

 

Les Nombres Carrés apparaissent dans le Théorème de Pythagore \(\large a^2 + b^2 = c^2\).

 

Différence de Carrés :

 

\(\large a^2 - b^2 = (a-b)(a+b)\).