Nombres

Les Nombres sont un concept large, utilisé fondamentalement pour indiquer une Quantité ou une Grandeur.

Il existe de nombreux Types de Nombres, qui sont divisés en Catégories. En Mathématiques nous travaillons avec tous, et ils peuvent être vus comme des Ensembles imbriqués, où chaque nouvelle Catégorie étend la précédente.

Voici ci dessous une brève description des Catégories les plus importantes.

 

Nombres Naturels \(\ N\)

Les Nombres Naturels sont tous les Nombres entiers supérieurs à zéro : 1, 2, 3, 4, 5, 6 … etc. Ils se notent \(\large N\). Dans certains contextes, on inclut aussi le 0, et alors on écrit \(\large N_0\).

 

Nombres Entiers \(\ Z\)

Si l’on étend les Nombres Naturels (y compris 0) avec les Nombres négatifs, on obtient les Nombres Entiers :

… -4, -3, -2, -1, 0, 1, 2, 3 … etc.

Ils se notent \(\large Z\).

 

Nombres Rationnels \(\ Q\)

Les Nombres Rationnels sont tous les Nombres qui peuvent s’écrire comme une Fraction, où le Numérateur est un Nombre Entier et le Dénominateur un Nombre Naturel différent de 0. Exemples :

 

\(\large \frac{1}{4} = 0,25\), \(\large -\frac{3}{5} = -0,6\)

 

Toutes les Fractions Décimales finies et périodiques appartiennent aussi ici.

Ils se notent \(\large Q\).

 

Nombres Réels \(\ R\)

Les Nombres Réels comprennent tous les Ensembles de Nombres mentionnés précédemment, mais aussi les Nombres Irrationnels, qui ne peuvent pas s’écrire comme des Fractions. Les Nombres Irrationnels ont un développement Décimal infini non périodique.

 

Exemples : \(\large \pi\) et \(\large \sqrt{5}\).

 

\(\large \sqrt{5} \) est un Nombre Réel, mais en même temps un Nombre Irrationnel, car il ne peut pas s’écrire comme une Fraction.

Les Nombres Réels se notent \(\large R\).

 

Nombres Complexes \(\ C\)

Les Nombres Complexes étendent les Nombres Réels en incluant les Nombres Imaginaires. Alors qu’un Nombre Réel peut être placé sur une Droite Numérique, un Nombre Complexe peut être représenté dans le Plan comme un Point avec les Coordonnées \(\large (x,y)\), où \(x\) est la Partie Réelle, et \(\large y\) est la Partie Imaginaire. Un Nombre Complexe s’écrit sous la forme :

 

\(\large z = x + yi \)

 

Ici \(i\) est l’Unité Imaginaire, définie par \(\large i^2 = -1\). Un exemple est :

 

\(\large z = 3 + 2i \)

 

Cela peut être compris comme le Point \(\large (3,2)\) dans le Plan Complexe.

Les Nombres Complexes sont utilisés par exemple pour résoudre des Équations qui n’ont pas de Solutions Réelles, comme :

 

\(\large x^2 + 1 = 0 \implies x = \pm i \)

 

Les Nombres Complexes se notent \(\large C\).

 

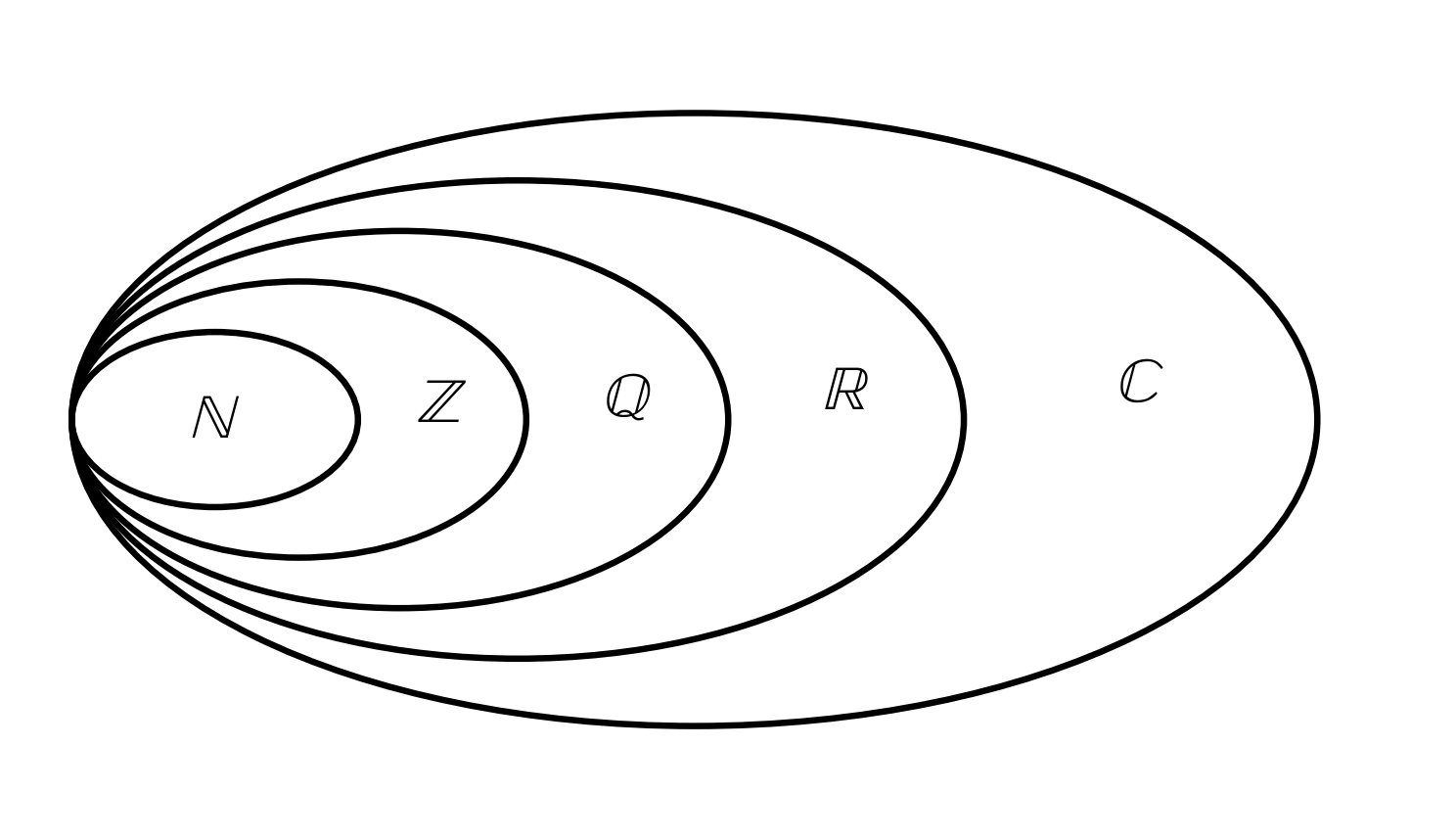
L’Image montre les Nombres Naturels comme une partie des Nombres Entiers, qui font eux mêmes partie des Nombres Rationnels, etc.

 

Résumé

La Hiérarchie entre les Ensembles Numériques peut s’écrire brièvement ainsi :

 

\(\Large N \subset Z \subset Q \subset R \subset C\)