Le triangle rectangle, comme son nom l’indique, a toujours un angle droit.

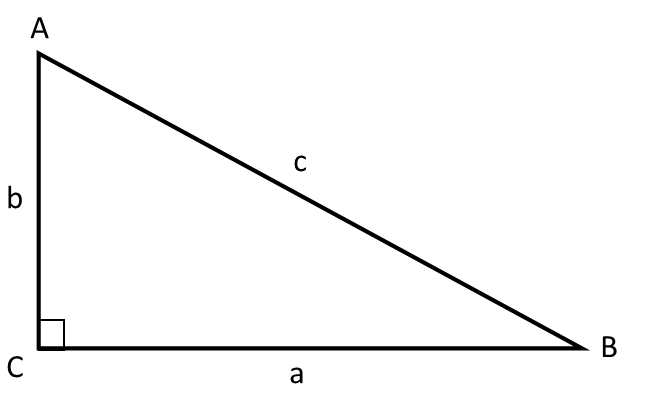
L’angle droit s’appelle angle C.

Les angles des triangles sont toujours désignés par des lettres majuscules, et les côtés par des lettres minuscules.

Côté a et côté b s’appellent cathètes et forment l’angle droit.

Côté c s’appelle l’hypoténuse et sera toujours le côté le plus long du triangle. 

Notez que côté a est opposé à angle A. 

Il en va de même pour côté b et côté c, et il en sera toujours ainsi.

Théorème de Pythagore

Le théorème de Pythagore décrit la relation entre les côtés d’un triangle rectangle.

Pythagore énonce que « le carré du côté a + le carré du côté b = le carré du côté c ».

$$ a^2 + b^2 = c^2 $$

Si nous avons un triangle où \(a = 3\) et \(b = 4\), nous obtenons ce qui suit :

$$ \begin{align} 3^2 + 4^2 &= c^2 \Leftrightarrow \\ 9 + 16 &= 25 \Leftrightarrow \\ c^2 &= 25 \Leftrightarrow \\ c &= \sqrt{25} = 5 \end{align} $$

Du théorème, on peut déduire deux formules pour calculer les côtés a et b :

$$ a = \sqrt{c^2 - b^2} $$

$$ b = \sqrt{c^2 - a^2} $$

Figure

La figure montre les carrés sur les côtés du triangle.

Vous pouvez lire sur le calcul des angles dans la section Trigonométrie.

Trigonométrie et triangles rectangles

Dans la section Trigonométrie, vous pouvez lire sur le cosinus, le sinus et la tangente.

Le cosinus, le sinus et la tangente peuvent être utilisés pour calculer les angles et les côtés dans les triangles rectangles.

SOUVENEZ-VOUS que vous ne devez pas utiliser ces formules pour les triangles qui ne sont pas rectangles.

Pour les autres triangles, vous devez utiliser les lois du cosinus et du sinus.

Quand on parle des côtés du triangle, on parle de la "cathète adjacente" et de la "cathète opposée".

Si vous regardez le dessin, vous pouvez voir que côté b est adjacent à angle A, donc c’est la cathète adjacente.

Côté a se trouve en revanche sur le côté opposé de angle A, donc c’est la cathète opposée.

Formules

Dans les triangles rectangles, on a :

$$ \cos(v) = \frac{\text{cathète adjacente}}{\text{hypoténuse}} $$

$$ \sin(v) = \frac{\text{cathète opposée}}{\text{hypoténuse}} $$

$$ \tan(v) = \frac{\text{cathète opposée}}{\text{cathète adjacente}} $$

En utilisant les fonctions trigonométriques inverses (arcsin, arccos, arctan), vous pouvez calculer l’angle directement :

$$ v = \cos^{-1}\biggl(\frac{\text{cathète adjacente}}{\text{hypoténuse}}\biggr) $$

$$ v = \sin^{-1}\biggl(\frac{\text{cathète opposée}}{\text{hypoténuse}}\biggr) $$

$$ v = \tan^{-1}\biggl(\frac{\text{cathète opposée}}{\text{cathète adjacente}}\biggr) $$