Triangles
Le premier polygone.
En géométrie plane, le triangle est le premier polygone. C'est la figure avec le moins de côtés.
Les éléments de base du triangle
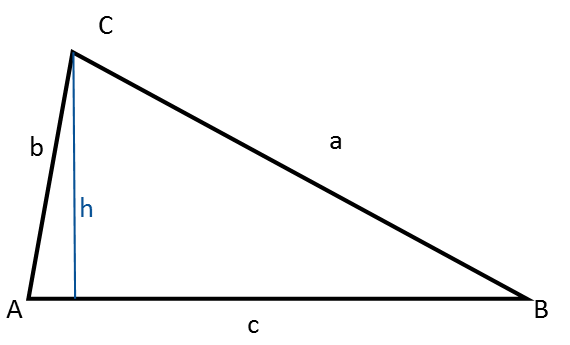
Un triangle a :
- Trois angles, toujours désignés par des lettres majuscules : A, B, C
- Trois côtés, toujours désignés par des lettres minuscules : a, b, c
- Une somme des angles de 180°
La hauteur dans un triangle
La hauteur dans un triangle est une ligne qui va perpendiculairement d’un sommet au côté opposé (la base).
Un triangle a trois hauteurs, une pour chaque côté, selon celui choisi comme base.
Types de triangles
Les triangles ne sont pas tous identiques, c’est pourquoi certains sont aussi plus faciles à calculer que d’autres.
Les triangles sont classés en différents types, selon leurs côtés et leurs angles.
Selon les angles :
- Si l’un des angles est de 90°, on l’appelle un triangle rectangle
- Si l’un des angles est supérieur à 90°, on l’appelle un triangle obtusangle
- Si tous les angles sont inférieurs à 90°, on l’appelle un triangle aiguangle
Selon les côtés :
- Si deux côtés sont de même longueur, on l’appelle un triangle isocèle
- Si les trois côtés sont de même longueur, on l’appelle un triangle équilatéral
Le triangle que vous voyez sur la figure ci-dessus est appelé un triangle quelconque.
- Il n’a aucun angle de 90°
- Il n’a aucun côté de même longueur.
- Tous les angles sont inférieurs à 90°, donc c’est aussi un triangle aiguangle
Un triangle peut avoir plusieurs propriétés. Par exemple, il peut être à la fois rectangle et isocèle.
Calcul des triangles
Les êtres humains calculent les triangles depuis des milliers d’années.
Les anciens Grecs travaillaient déjà avec la géométrie bien avant notre ère.
L’un des plus célèbres était Pythagore, qui a formulé le théorème de Pythagore – une méthode pour calculer les côtés d’un triangle rectangle.
Plus tard, la trigonométrie est apparue, une branche des mathématiques permettant de calculer les angles et les côtés de tous les types de triangles.
La trigonométrie a été développée à l’origine par des astronomes grecs, puis perfectionnée par des mathématiciens du monde entier. Aujourd’hui, elle est utilisée dans des domaines tels que l’architecture et l’exploration spatiale.