Triangle équilatéral

Dans un triangle équilatéral, les trois côtés ont la même longueur.

Ainsi, les angles sont également toujours égaux.

Image d’un triangle équilatéral

La somme des angles dans un triangle est toujours de 180^o, il est donc possible de calculer l’angle sans rien savoir d’autre sur le triangle.

Il suffit de diviser 180 par 3 :

$$ \frac{180^\circ}{3}=60^\circ $$

Les angles d’un triangle équilatéral sont toujours de 60 degrés.

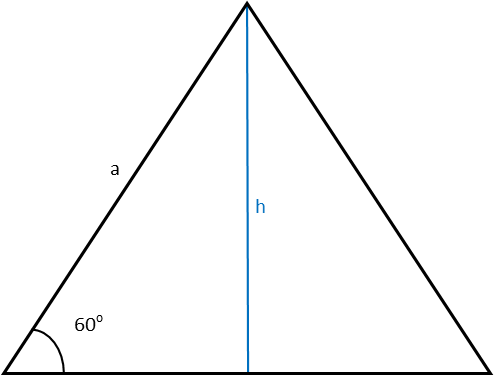
Si l’on connaît la hauteur ou la longueur d’un côté, il est possible de calculer le reste du triangle.

La hauteur divise le triangle en deux triangles rectangles égaux, il est donc possible d’utiliser les formules des triangles rectangles.

Calculatrice

$$ a=\frac{P}{3} $$

$$ a=\frac{h}{sin(60)} $$

$$ a=2\cdot \frac{Area}{h} $$

$$ h = cos(30)\cdot a $$

$$ h=sin(60)\cdot a $$

$$ h = \frac{\sqrt{3}}{2} \cdot a $$

$$ h=\sqrt{a^2- \biggl( \frac{a}{2}\biggr)^2} $$

$$ h= \frac{2\cdot Area}{a} $$

$$ A=\frac{h\cdot a}{2} $$

$$ A=\frac{\sqrt{3}}{4}\cdot a^2 $$

$$ A= \frac{1}{2} \cdot \sqrt{a^4 - \biggl( \frac{a^2}{2}\biggr)^2} $$

$$ P=3\cdot a $$

$$ P= 3\cdot \frac{h}{sin(60)} $$