Triangle scalène
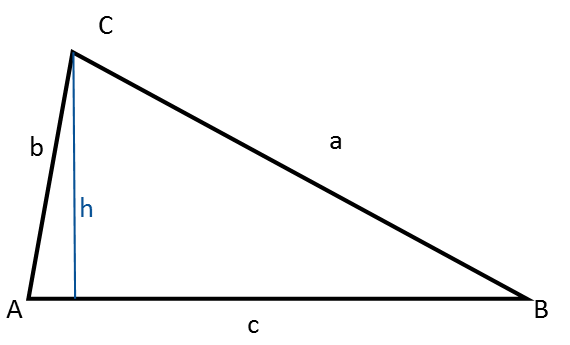
Un triangle scalène est un triangle dont tous les côtés et tous les angles sont différents, c’est-à-dire qu’il n’est ni rectangle, ni isocèle, ni équilatéral.
Formules et méthodes
Pour calculer les triangles scalènes, il faut utiliser les relations du cosinus et du sinus.
Attention, l’utilisation de la relation du sinus peut entraîner une ambiguïté, dans certains cas deux triangles différents peuvent correspondre aux données et donc donner deux solutions.
Pour en savoir plus sur les relations du cosinus et du sinus, consulte Trigonométrie.
Pour pouvoir calculer un triangle scalène, il faut connaître une longueur de côté et au moins deux autres informations sur le triangle.
Dans certains cas, la hauteur du triangle peut être utilisée à la place d’un côté dans les calculs.
Note que la hauteur du triangle le divise en deux triangles rectangles. Cela peut être utile dans certains calculs car cela permet d’utiliser la trigonométrie des triangles rectangles et le théorème de Pythagore.
Mais RAPPELLE-TOI : Tu ne dois pas utiliser les formules des triangles rectangles si le triangle n’est pas rectangle !
On ne peut les utiliser que si le triangle est divisé en deux triangles rectangles et que tu calcules sur ceux-ci.
À droite, tu trouveras toutes les formules pour calculer les triangles scalènes.