Cercle circonscrit

Dans tout triangle, on peut tracer un cercle qui passe par les trois sommets du triangle.

 

On l’appelle le cercle circonscrit.

 

 

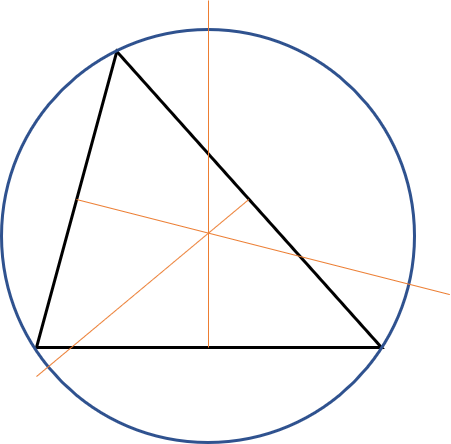
Médiatrices et centre

Une médiatrice est une droite perpendiculaire à un segment qui le coupe en son milieu.

Les médiatrices divisent les trois côtés du triangle (a, b, c) et se croisent au centre du cercle circonscrit.

Pour tracer un cercle circonscrit, commence par tracer les trois médiatrices. Au point d’intersection, place ton compas et tu peux tracer le cercle.

 

Rayon et aire

Le rayon du cercle circonscrit peut être calculé avec la formule suivante :

 

$$ \large r=\frac{a \cdot b \cdot c}{4 \cdot A} $$

 

Où \(\large A\) est l’aire du triangle.

Si tu veux calculer l’aire du triangle, tu peux inverser la formule :

 

$$ \large A=\frac{a \cdot b \cdot c}{4 \cdot r} $$

 

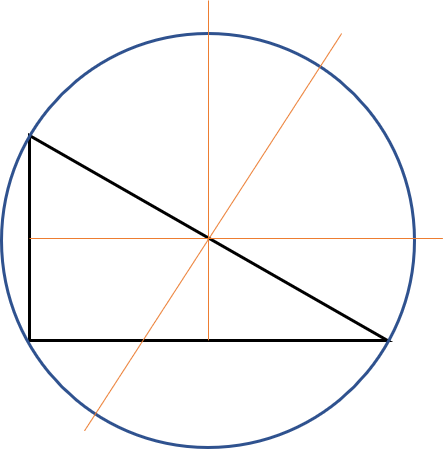
Triangle rectangle

Le cercle circonscrit d’un triangle rectangle a toujours son centre exactement au milieu de l’hypoténuse.

Cela rend aussi plus facile de trouver le rayon, qui est la moitié du côté c :

 

$$ \large r=\frac{c}{2} $$