Trigonometriske funktioner

Trigonometriske funktioner er funktioner, der bygger på forholdene i en retvinklet trekant. De tre mest kendte trigonometriske funktioner er sinus, cosinus og tangens.

 

Disse funktioner er periodiske, hvilket betyder, at de gentager sig med faste intervaller. De spiller en central rolle i matematik, fysik og teknik, særligt i forbindelse med bølger, rotationer og vinkler.

 

Sinusfunktion

Sinusfunktionen beskriver forholdet mellem modstående katete og hypotenusen i en retvinklet trekant.

Den skrives på denne form:

 

$$ \Large y = \sin(x) $$

 

Karakteristika:

  • Perioden er \(2\pi\)
  • Amplituden er 1
  • Starter i \((0,0)\)
  • Kurven svinger mellem -1 og 1

 

Eksempel: Værdier for \(\large y = \sin(x) \)

\(\Large x\) 0 \(\Large \tfrac{\pi}{2}\) \(\Large \pi\) \(\Large \tfrac{3\pi}{2}\) \(\Large 2\pi\)
\(\Large y\) 0 1 0 -1 0

 

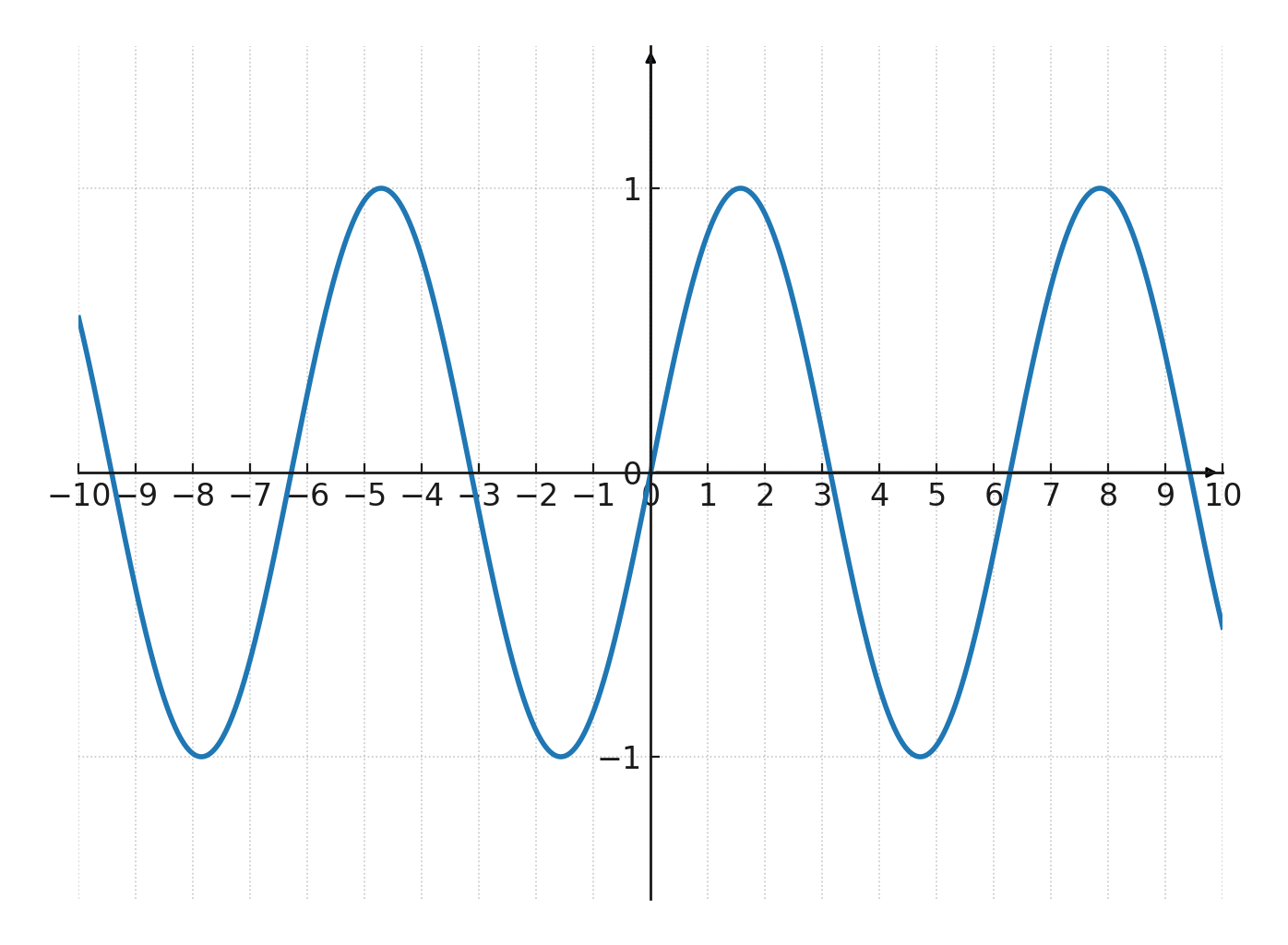
Sinus funktion

 

Cosinusfunktion

Cosinusfunktionen beskriver forholdet mellem hosliggende katete og hypotenusen i en retvinklet trekant.

Den skrives på denne form:

 

$$ \Large y = \cos(x) $$

 

Karakteristika:

  • Perioden er \(2\pi\)
  • Amplituden er 1
  • Starter i \((0,1)\)
  • Kurven svinger mellem -1 og 1

 

Eksempel: Værdier for \(\large y = \cos(x) \)

\(\Large x\) 0 \(\Large \tfrac{\pi}{2}\) \(\Large \pi\) \(\Large \tfrac{3\pi}{2}\) \(\Large 2\pi\)
\(\Large y\) 1 0 -1 0 1

 

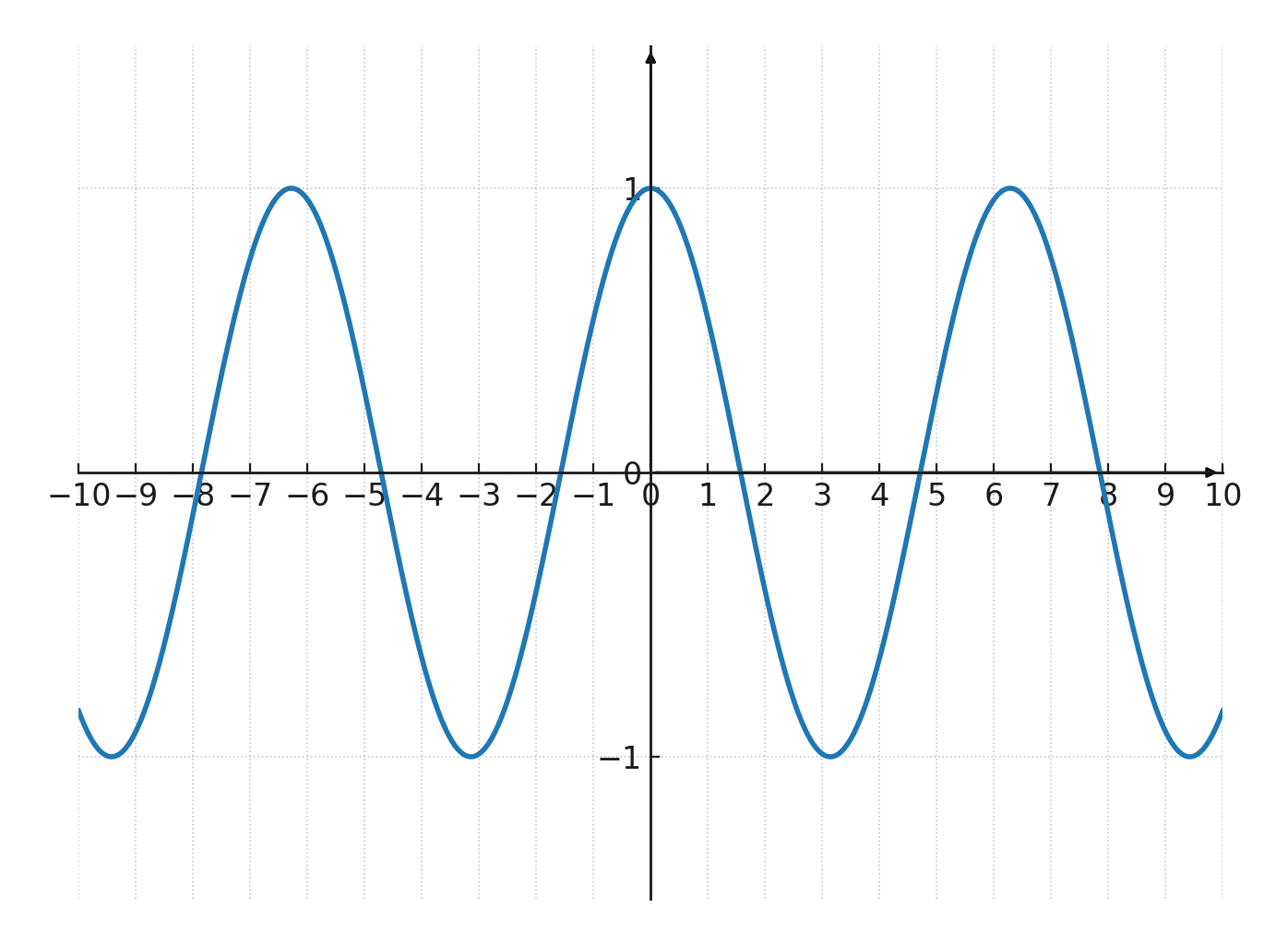
Cosinus funktion

 

Tangensfunktion

Tangensfunktionen beskriver forholdet mellem modstående katete og hosliggende katete i en retvinklet trekant.

Den skrives på denne form:

 

$$ \Large y = \tan(x) $$

 

Karakteristika:

  • Perioden er \(\pi\)
  • Ingen amplitude (funktionen kan blive uendeligt stor eller lille)
  • Asymptoter ved \( x = \tfrac{\pi}{2}, \tfrac{3\pi}{2}, \ldots \)
  • Starter i \((0,0)\)

 

Eksempel: Værdier for \(\large y = \tan(x) \)

\(\Large x\) -\(\Large \tfrac{\pi}{4}\) 0 \(\Large \tfrac{\pi}{4}\) \(\Large \tfrac{\pi}{2}\)
\(\Large y\) -1 0 1 uendelig

 

 

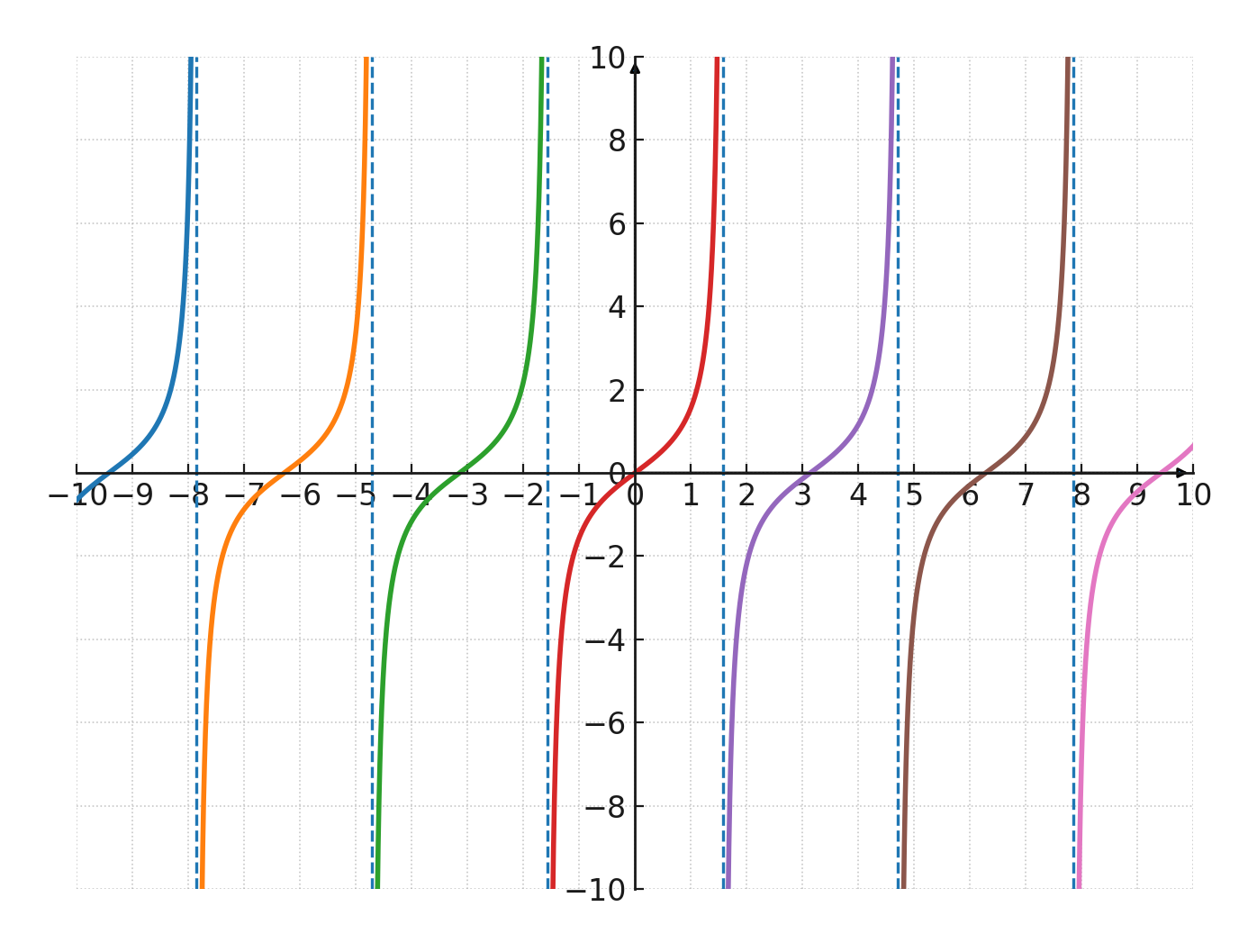
Tangens funktion

 

Opsummering

Sinus, cosinus og tangens er alle trigonometriske funktioner med forskellige egenskaber, men de hænger sammen.

 

  • Sinus starter i 0 og beskriver svingningen op og ned
  • Cosinus starter i 1 og er forskudt i forhold til sinus
  • Tangens har asymptoter og gentager sig med kortere periode

 

De tre funktioner bruges ofte sammen til at beskrive vinkler, bevægelse og periodiske fænomener i matematik og naturvidenskab.