Koordinatsystemet

Et koordinatsystem består af to tallinjer, der står vinkelret på hinanden. Tallinjerne kaldes for akser.

Den vandrette akse kaldes for x-aksen eller førsteaksen, og den lodrette akse kaldes for y-aksen eller andenaksen.

De to akser skærer hinanden i deres 0-punkt. Punktet kaldes origo.

 

 

Punkter i koordinatsystemet

Et punkt i koordinatsystemet kan aflæses ved at følge en vinkelret linie til akserne og aflæse henholdsvis x- og y-aksens værdi netop der. X-aksen læses altid først, så et punkt beskrives som \( \large (x,y)\).

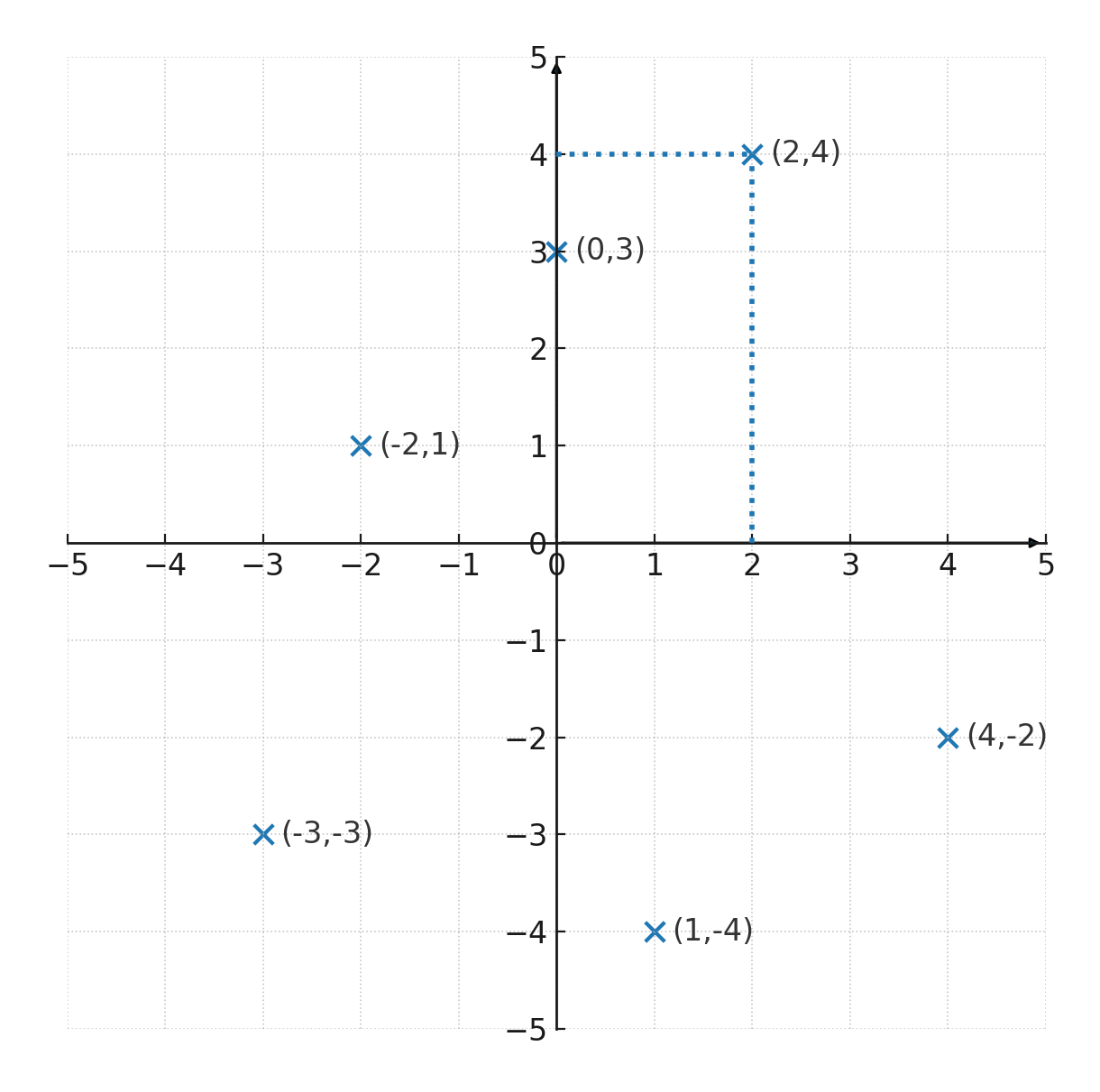
I nedenstående koordinatsystem er indtegnet forskellige punkter.

Punktet \( \large (2,4)\) ligger i koordinatsystemet, hvor de to vinkelrette linjer viser, at:

• x-aksen = 2
• y-aksen = 4

 

 

 

Kvadranter

De fire områder i Koordinatsystemet kaldes kvadranter, hvor:

 

• 1. kvadrant: \( \large (x,y)\)
• 2. kvadrant: \( \large (-x,y)\)
• 3. kvadrant: \( \large (-x,-y)\)
• 4. kvadrant: \( \large (x,-y)\)

 

Tre dimensioner

Koordinatsystemet kan også udvides til tre dimensioner ved at tilføje en z-akse, som står vinkelret på x- og y-aksen i origo.  

I det todimensionelle system findes der fire kvadranter, men i det tredimensionelle system opdeles rummet i otte områder, som kaldes oktanter.

Punkter angives med tre tal \( (x,y,z) \). Dette bruges fx i rumgeometri.