Funktioner

En funktion bruges til at beskrive en sammenhæng mellem ting. Hvis én ting ændrer sig, så ændrer noget andet sig også.

 

Hvis du tager en is ud af fryseren og lader den ligge, så vil den langsomt smelte, efterhånden som tiden går, fordi den bliver varmere.
Der er altså en sammenhæng mellem tiden der går, og temperaturen der stiger.

 

Det kunne også være prisen på is. Hvis du køber én is, koster den 5 kroner. Hvis du køber to is, koster de 10 kroner osv.

En funktion der kan beregne prisen på is, ser sådan ud:

 

$$ \large y=5x $$

 

Hvor \(\large x\) er antal is, og \(\large y \) er prisen.

 

Funktionen er et 1. grads polynomium (lineær funktion).

Den er også en proportional funktion, fordi den altid vil gå gennem origo (punktet \((0,0)\)).

 

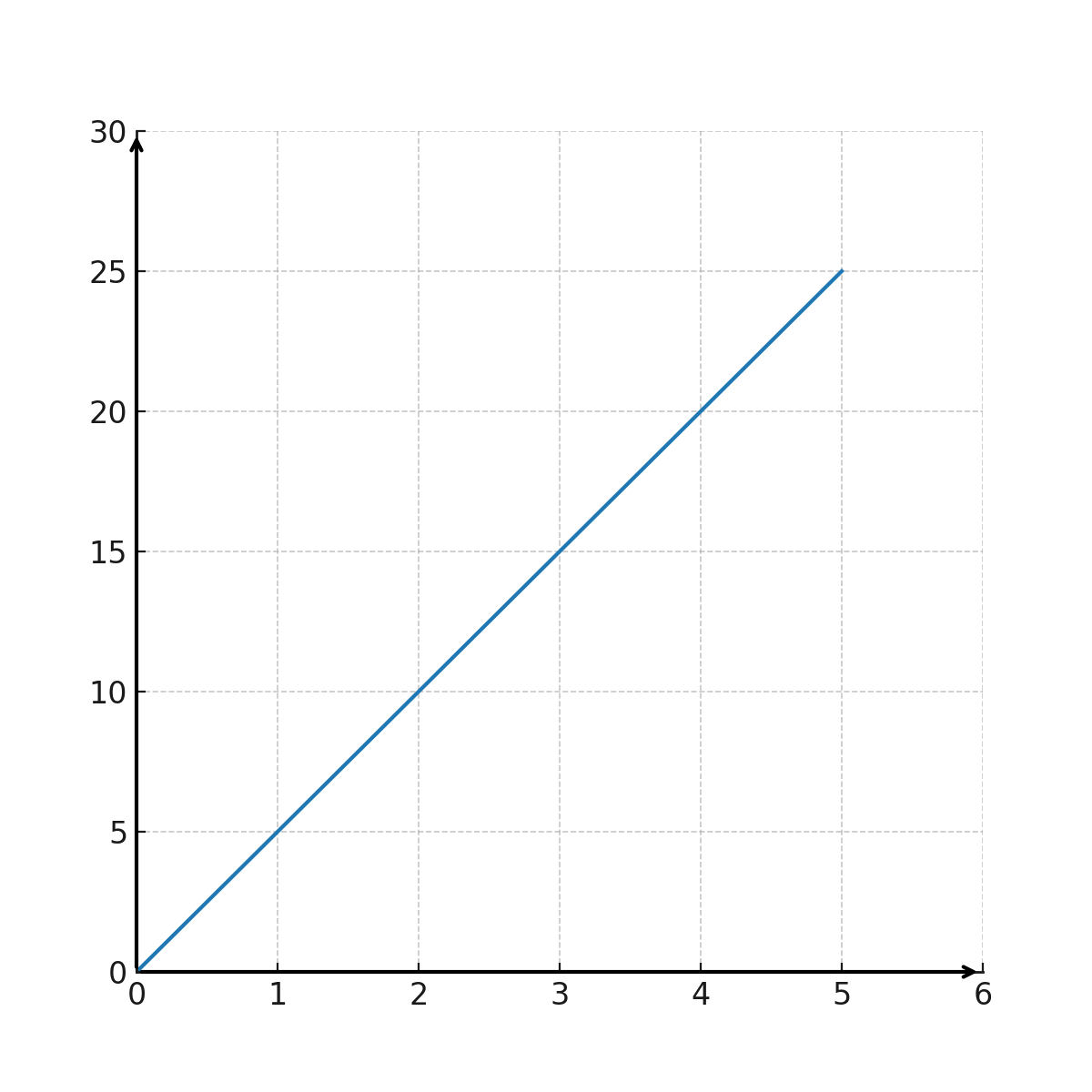
Grafen viser udviklingen i prisen på is

Antal is på X-aksen og prisen på Y-aksen

 

At tegne en graf

Når man skal tegne funktionen som en graf i et koordinatsystem, kalder man \(\large x\) for uafhængig variabel (antal is), og \(\large y\) for afhængig variabel (prisen).

Hver gang du indsætter en værdi for  \(\large x\) i din funktion, kan du beregne den tilsvarende værdi for  \(\large y\) og dermed sætte et punkt ind i koordinatsystemet.

 

Eksempel:

• Hvis du sætter \(\large x=1 \) is ind i funktionen, får du \(\large y=5 \).

• Hvis du sætter \(\large x=5 \) is ind i funktionen, får du \(\large y=25\).

 

Nu har vi to koordinatsæt \(\large (1,5)\) og \(\large (5,25)\). Når de tegnes i koordinatsystemet og forbindes med en ret linje gennem origo, får vi grafen ovenfor.