Rationale funktioner

En rationel funktion er en brøk, hvor både tæller og nævner er polynomier. Man kan altså skrive en rationel funktion som:

$$ \large f(x) = \frac{P(x)}{Q(x)} $$

Her er $P(x)$ og $Q(x)$ polynomier, og nævneren $Q(x)$ må ikke være lig med 0.

Rationale funktioner kan have lodrette asymptoter der, hvor nævneren bliver 0, og de kan have vandrette eller skrå asymptoter, afhængigt af graden af tælleren og nævneren.

Eksempel på en rationel funktion

Et eksempel på en rationel funktion er:

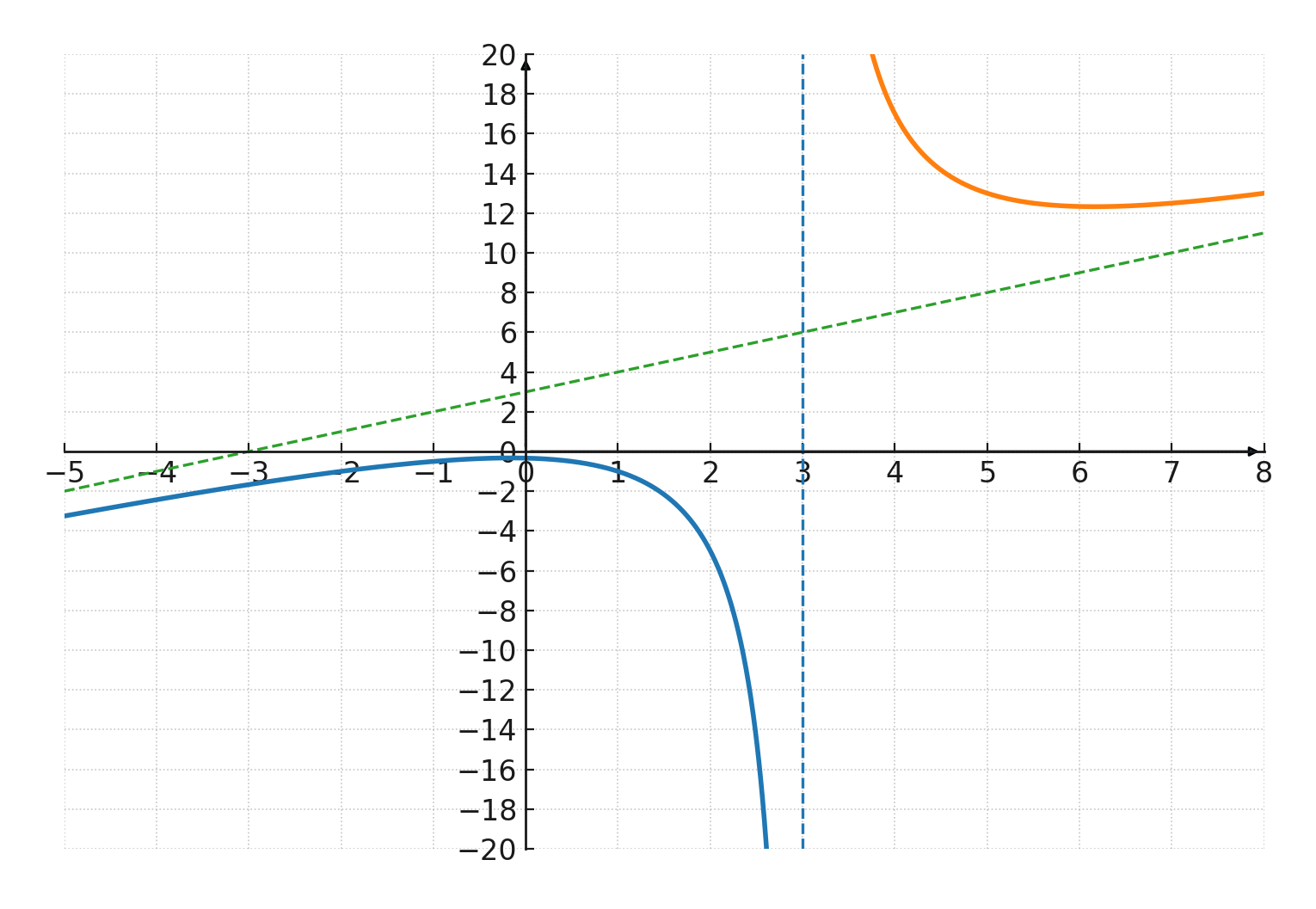
$$ \large f(x) = \frac{x^2+1}{x-3} $$

I dette eksempel er tælleren $x^2+1$, som er et 2. grads polynomium, og nævneren $x-3$, som er et 1. grads polynomium.

Funktionen er ikke defineret for $x=3$, fordi man ikke må dividere med 0.
Grafen har derfor en lodret asymptote ved $x=3$.
Når $x$ bliver meget stor eller meget lille, opfører brøken sig omtrent som $\tfrac{x^2}{x} = x$. Derfor har grafen en skrå asymptote, der ligger tæt på linjen $y=x$.

Rational funktion

Omvendt proportionalitet

En af de simpleste typer af rationale funktioner er den omvendt proportionale funktion:

$$ \large f(x) = \frac{k}{x} $$

Her er $k$ en konstant. Funktionen er ikke defineret for $x=0$, fordi man ikke kan dividere med nul.

Grafen har en karakteristisk form, hvor den ligger i 1. og 3. kvadrant, hvis $k$ er positiv, og i 2. og 4. kvadrant, hvis $k$ er negativ.

Denne funktion kaldes omvendt proportional, fordi når $x$ bliver dobbelt så stor, bliver $f(x)$ halvt så stor. Produktet $x \cdot f(x)$ er altid det samme (lig med $k$).