Omvendt proportional funktion

En funktion er omvendt proportional, når følgende er gældende:

 

$$ y \cdot x=k $$

 

Det vil sige at hvis man ganger de to koordinater, x og y, med hinanden, så giver alle koordinatsæt det samme resultat (k).

 

Feks følgende koordinatsæt:

 

$$ (1,20) = 1 \cdot 20 = 20 $$

$$ (2,10) = 2 \cdot 10 = 20 $$

$$ (4,5) = 4 \cdot 5 = 20 $$

$$ (5,4) = 5 \cdot 4 = 20 $$

$$ (10,2) = 10 \cdot 2 = 20 $$

$$ (20,1) = 20 \cdot 1 = 20 $$

 

Tegner man disse koordinatsæt ind i et system får man nedenstående kurve, som altid har asymptoter langs begge akser.

Det vil sige, at den kan komme meget tæt på akserne, men vil aldrig skære dem.

 

 

 

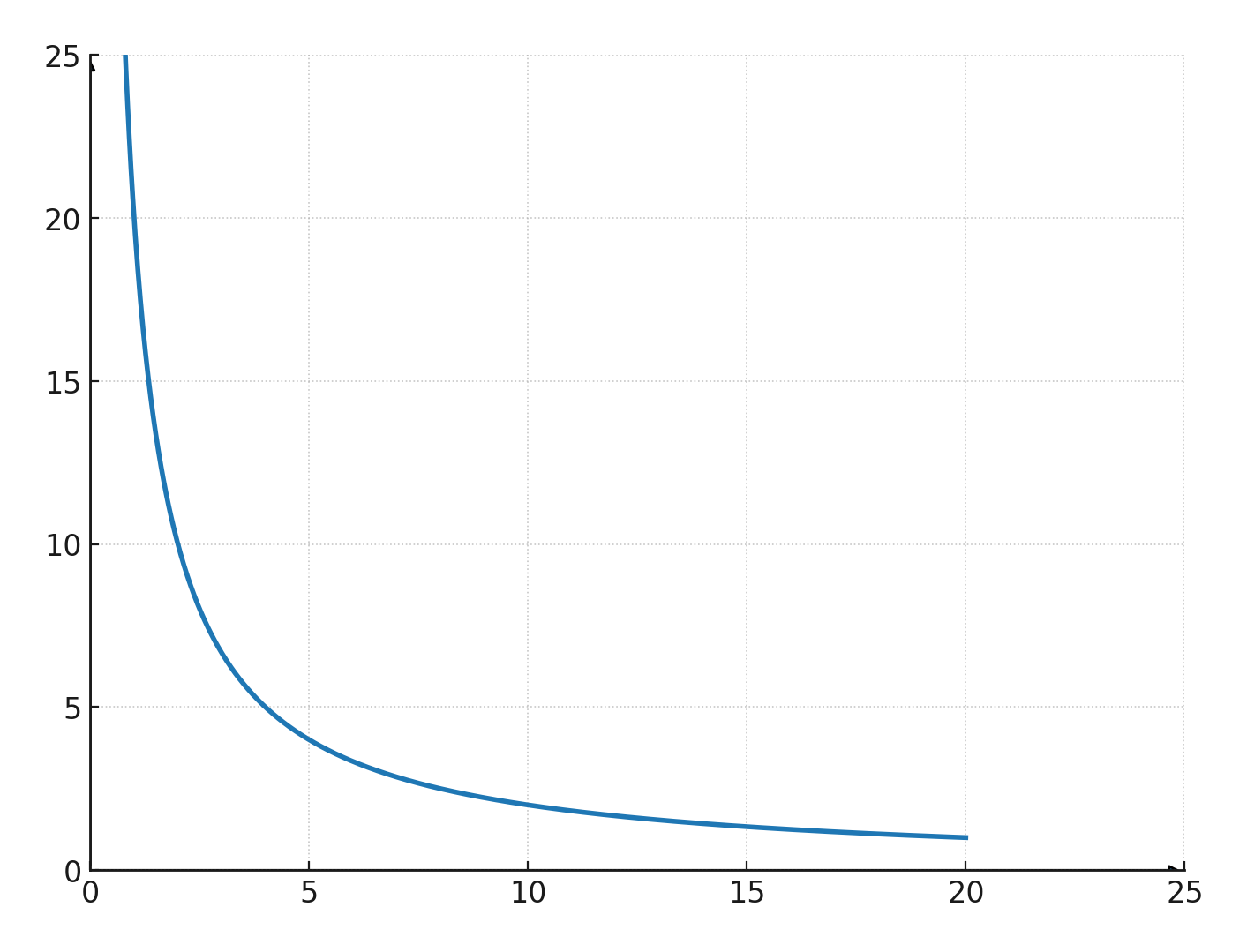
Konstanten k

k kaldes for proportionalitetskonstanten.

Funktionsforskriften for omvendt proportionalitet skrives sådan her:

 

$$ f_{(x)} = \frac{k}{x} $$

 

\( x \) kan ikke være 0. Man kan ikke dividere med 0.

Hvis konstanten er 15 og x = 5, så er y = 3

 

$$ y = \frac{15}{5} $$

$$ y = 3 $$

 

På den måde kan du regne flere koordinatsæt, med samme konstant (15).

Bemærk at hvis du har fundet koordinat \((5,3)\), så gælder også \((3,5)\)

 

Du kan også gøre det med x = -5, så bliver y = -3

 

$$ y = \frac{15}{-5} $$

$$ y = -3 $$

 

Hvis du gør det med negative tal, vil du kunne tegne en kurve mere, som er en spejling af den første.

Disse kurver kaldes for en Hyperbel.

 

 

Hyperbel

Herunder er tegnet en hyperbel med konstanten 15

Koordinater for kurven i 1. kvadrant er indsat i værditabellen:

 

\(\Large x \)	1	2	3	5	6	10	15
\(\Large y \)	15	7,5	5	3	2,5	1,5	1

 

 

 

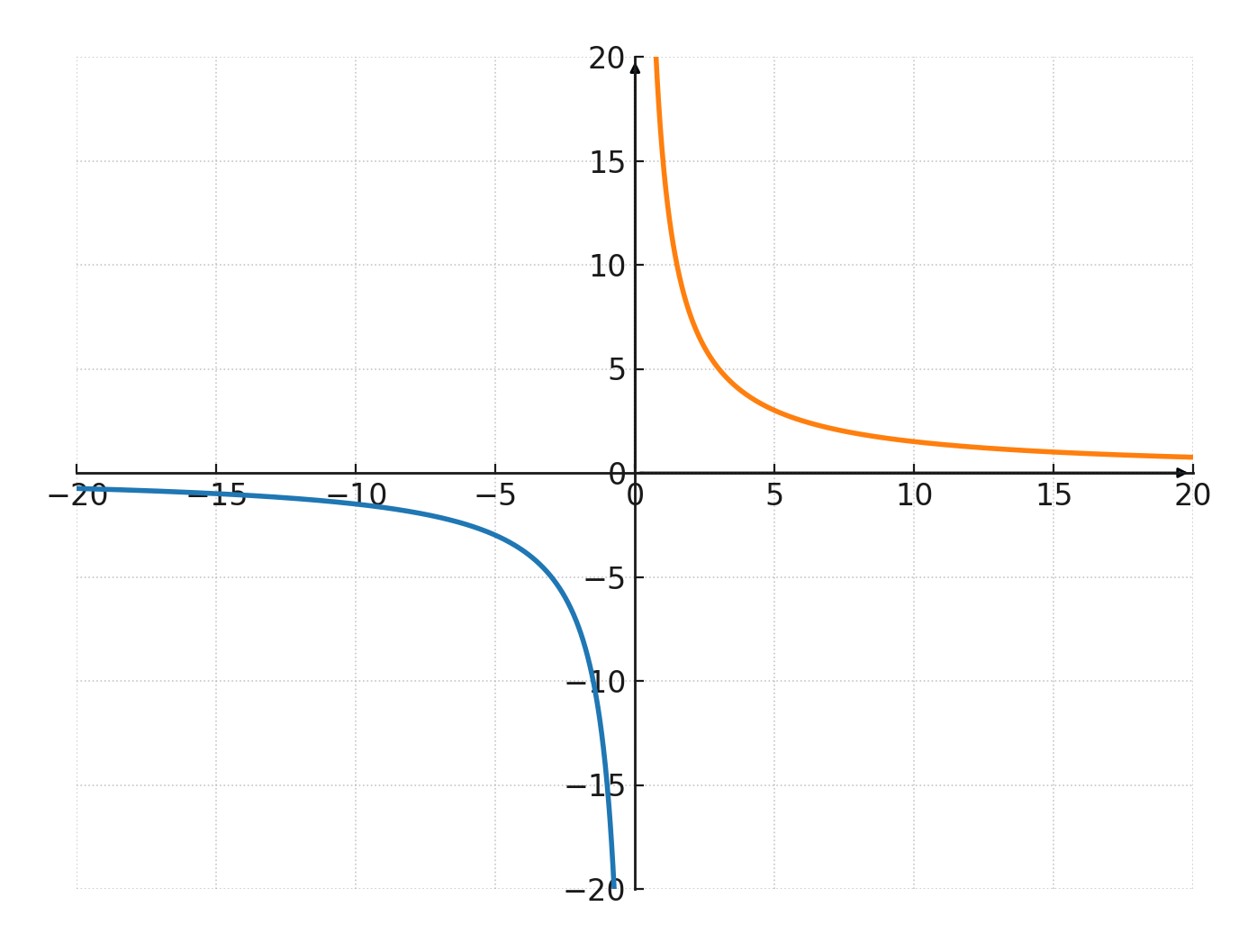
For kurven i 3. kvadrant gælder også at \( x \cdot y = 15\)

 

\(\Large x \)	-1	-2	-3	-5	-6	-10	-15
\(\Large y \)	-15	-7,5	-5	-3	-2,5	-1,5	-1

 

I eksemplet her er udeladt nogle koordinater af pladshensyn. Du bør lave koordinatsæt for alle x fra 1-15.

Så kan du tegne en mere præcis kurve.