Asymptoter

En asymptote er en linje, som grafen for en funktion kommer tættere og tættere på, uden nogensinde at skære den (eller kun i enkelte punkter). For rationale funktioner er asymptoter meget almindelige.

 

Der findes tre typer asymptoter:

 

Lodrette asymptoter:

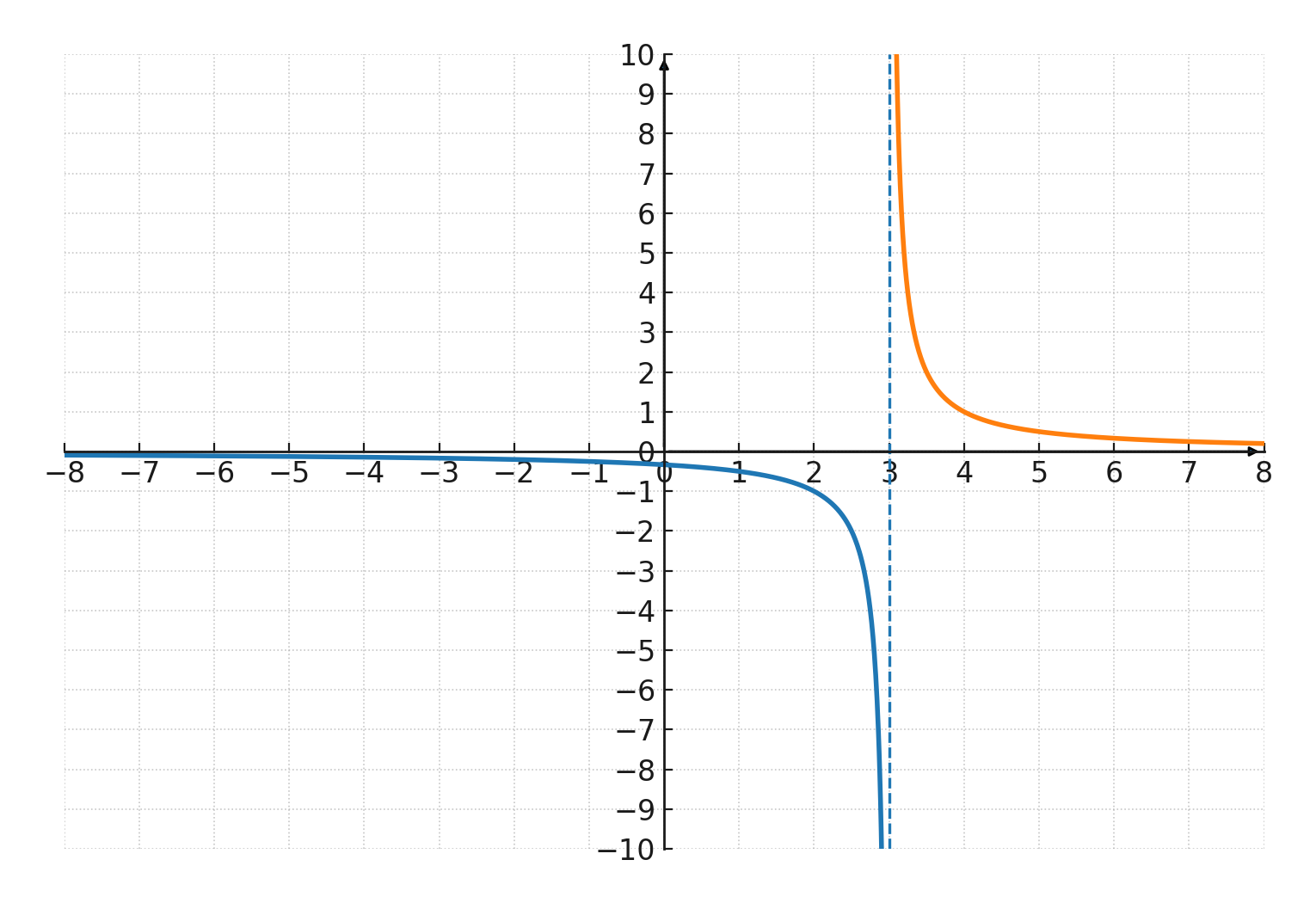
Opstår, hvor nævneren i en rationel funktion bliver 0. For eksempel har funktionen \( \Large f(x) = \frac{1}{x-3} \) en lodret asymptote ved \(\large x = 3 \).

Funktionen har desuden x-aksen som en vandret asymptote.

 

Vandrette asymptoter:

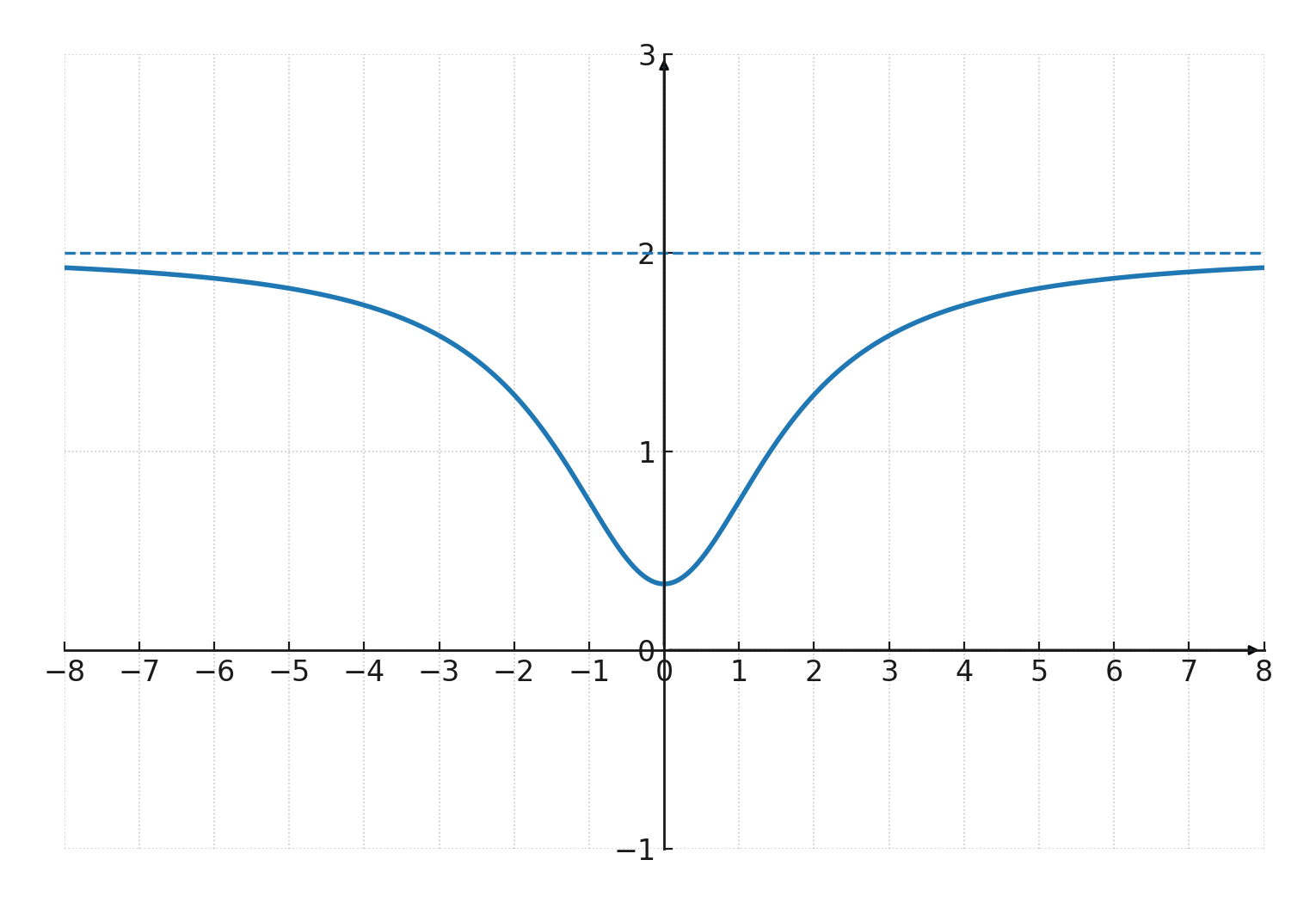
Opstår, når grafen for en funktion nærmer sig en konstant værdi, når \(\large x \) bliver meget stor eller meget lille.

For eksempel har \(\Large f(x) = \frac{2x^2+1}{x^2+3} \) en vandret asymptote ved \(\large y = 2 \).

 

 

Skrå asymptoter:

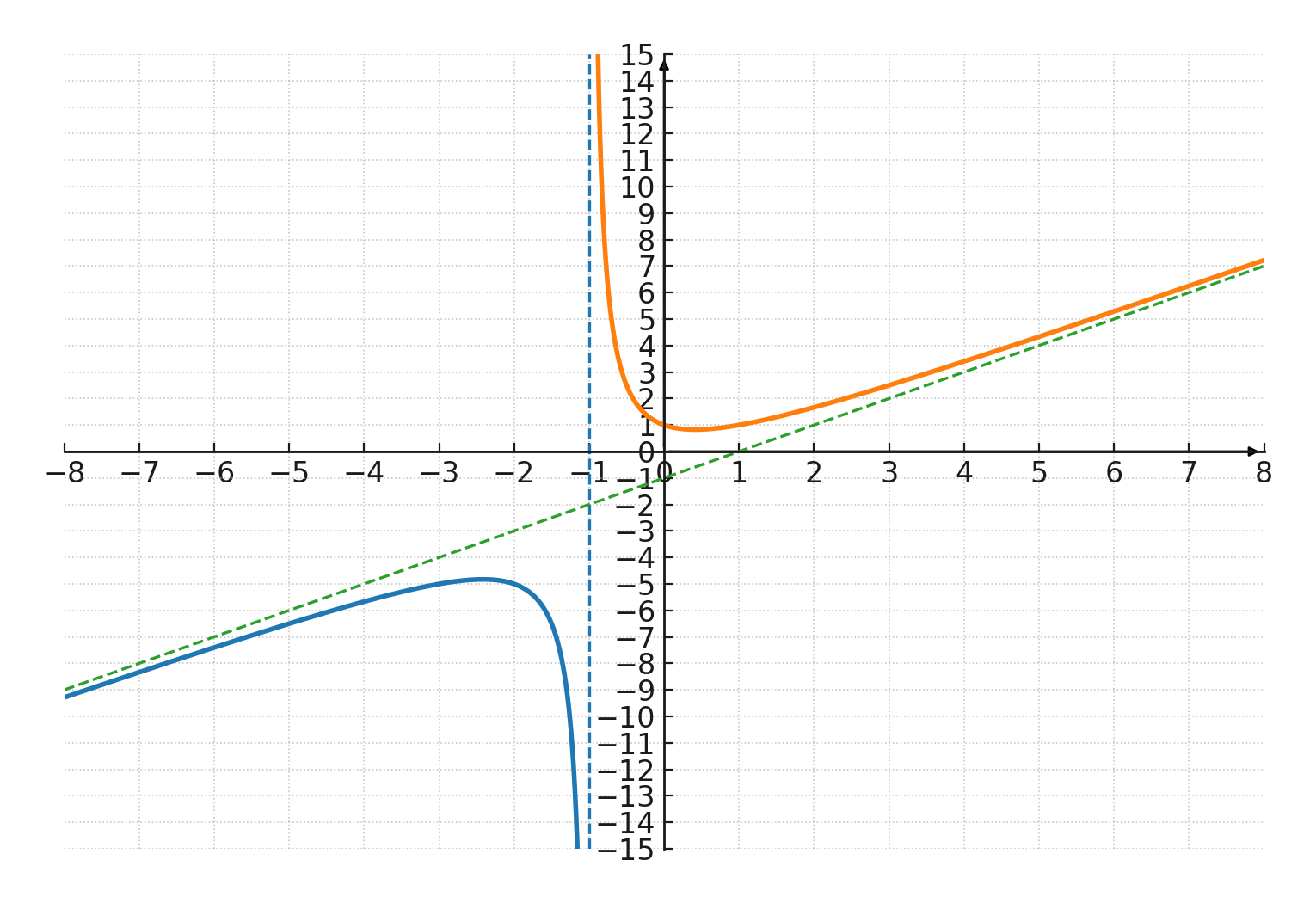
Opstår, når graden af tælleren er præcist 1 højere end graden af nævneren.

For eksempel har \(\Large f(x) = \frac{x^2+1}{x+1} \) en skrå asymptote ved linjen \(\large y = x - 1 \).

 

 

Asymptoter hjælper os med at forstå udviklingen af en graf, uden at tegne den fuldstændigt.