Polynomier

Et polynomium er en bestemt type matematisk funktion, der er bygget op af led, hvor en variabel (typisk kaldet x) opløftes i forskellige potenser og ganges med tal (koefficienter). Til sidst kan man lægge flere af disse led sammen.

 

Den simpleste type polynomium er en konstant funktion. Det kaldes et polynomium af 0. grad, fordi der ikke indgår nogen x. Funktionen har altid den samme værdi, uanset hvad x er.

Et eksempel er:

 

$$ \large f(x) = 5 $$

 

Her er værdien altid 5, uanset om x er -10, 0 eller 100. Grafen bliver derfor en vandret linje parallelt med x-aksen.

 

Her et eksempel på et polynomium af 2. grad. Den kaldes også en kvadratisk funktion:

 

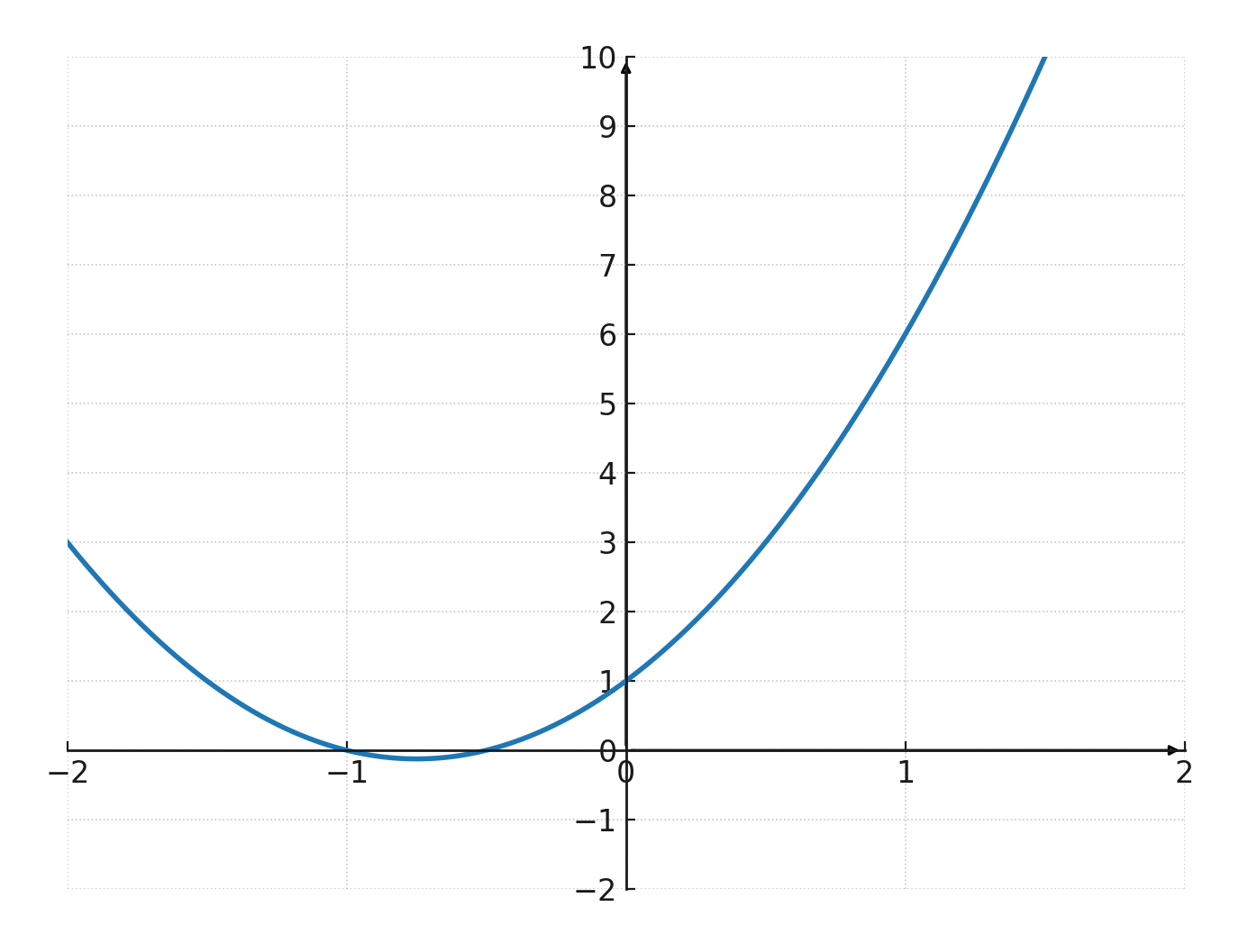
$$ \large f(x) = 2x^2 + 3x + 1 $$

 

Her er der tre led: \(2x^2\), \(3x\) og \(1\).  Hvis man tegner den som en graf, vil det blive til en parabel:

 

 

 

Graden af et polynomium

Det højeste tal på x (eksponenten) kaldes polynomiets grad:

 

• 0. grad: Konstant funktion, fx \( f(x)=5 \).
• 1. grad: Lineær funktion, fx \( f(x)=2x+1 \).
• 2. grad: Kvadratisk funktion, fx \( f(x)=x^2-3x+2 \).
• 3. grad: Kubisk funktion, fx \( f(x)=x^3-3x+2 \).

 

Fra 4. grad og opefter bruger man normalt bare betegnelsen n-te grads polynomium i stedet for et særligt navn.

 

Jo højere grad, desto mere komplekse bliver graferne, og kurverne kan bøje på flere måder.

 

En uendelig familie

Polynomier udgør en hel familie af funktioner.

Der findes polynomier af alle grader, og derfor kan man sige, at det i princippet er en uendelig række af funktioner. Hvert polynomium har sin egen særlige graf, afhængigt af graden og de tal, der bruges som koefficienter.

 

Hvor bruges polynomier?

Polynomier er vigtige, fordi de dukker op mange steder i matematik og i virkeligheden:

 

• I økonomi kan en funktion bruges til at beskrive udvikling i rente eller investering.
• I fysik kan en funktion beskrive bevægelse eller hastighed.
• I statistik kan de hjælpe med at tilpasse kurver til data.

 

Selv om polynomier lyder tekniske, er de altså grundlæggende byggeklodser i matematikken, og de giver os redskaber til at beskrive og forstå alt fra en simpel ret linje til meget mere komplicerede sammenhænge.