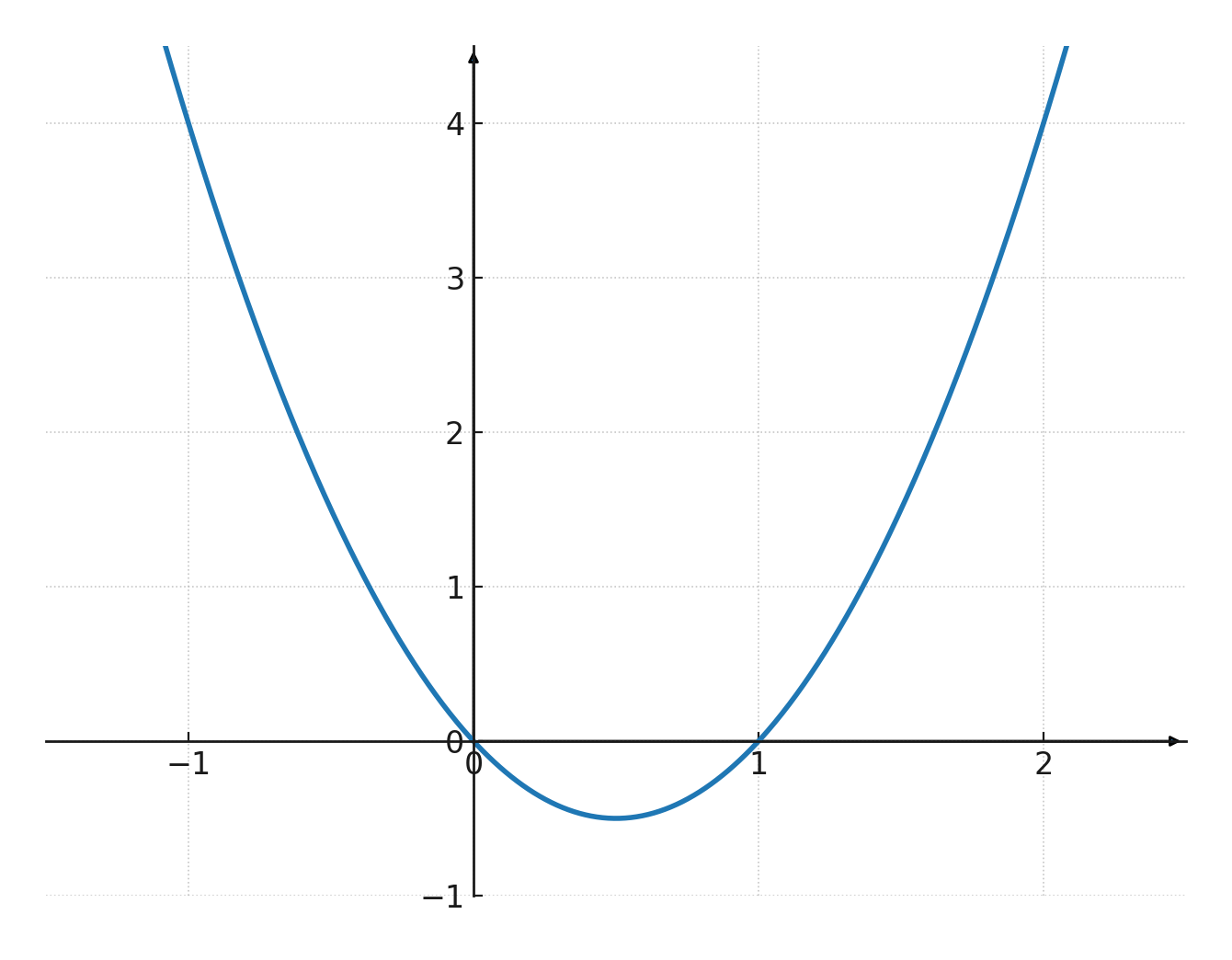
Kvadratisk funktion
Hvor en lineær funktion er en førstegradsfunktion, er en kvadratisk funktion er en andengradsfunktion og skrives på denne form:
$$ \large f(x)=a \cdot x^2 + b \cdot x + c $$
\(\large a\) kan ikke være 0. Hvis vi sætter 0 ind og ganger, så bliver det ingenting. Leddet forsvinder og tilbage står en lineær funktion
Hvis du tegner en kvadratisk funktion som graf, bliver den til en parabel, hvor følgende gælder:
- Hvis \(\large a>0\) vil benene vende opad
- Hvis \(\large a<0\) vil benene vende nedad
- Parablen vil altid skære y-aksen i \(\large (0,c) \)
- \(\large a \) bestemmer hvor stejl parablen er, jo større \(\large a \) er, desto smallere bliver parablen
- Parablen altid er symmetrisk om en lodret linje gennem toppunktet (parablens symmetriakse)
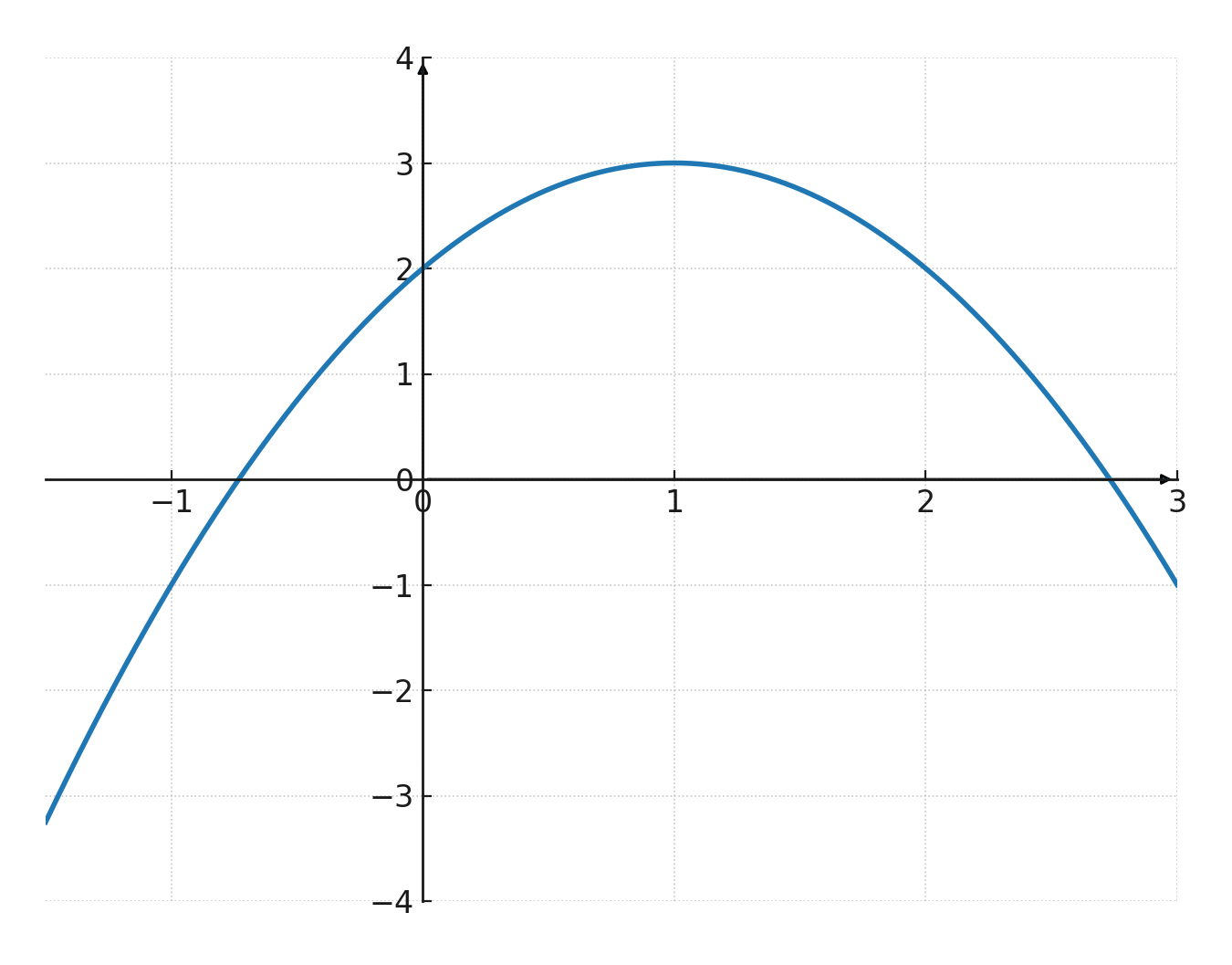
Toppunkt og skæringspunkt
En kvadratisk funktion hænger sammen med andengradsligninger.
For at finde skæringspunktet med X-aksen, skal du løse andengradsligningen, hvor \( y=0\):
$$ \large 0=ax^2+bx+c $$
Du skal gøre som du plejer, når du regner andengradsligninger
Diskriminanten vil fortælle dig lidt om parablens skæringspunkt:
- Hvis \( D > 0\) skærer den X-aksen to steder
- Hvis \( D < 0\) skærer den ikke X-aksen
- Hvis \( D = 0\) skærer den kun X-aksen én gang
For at beregne toppunktet i en parabel, skal vi også bruge diskriminaten:
$$ \large D= b^2-4ac $$
Når vi har diskriminanten, kan vi regne \((\large x,y)\) for toppunktet:
$$ \large x=\frac{-b}{2a} $$
$$ \large y=\frac{-D}{4a} $$
Eksempel skæringspunkt
Vi prøver funktionen \(\large y=2x^2-2x+0\)
Først finder vi diskriminanten:
$$ D=b^2-4ac \Leftrightarrow $$
$$ D=2^2-4 \cdot 2 \cdot 0 \Leftrightarrow $$
$$ D=4 $$
Diskriminanten er positiv.
Det betyder at parablen vil skære x-aksen to steder. Vi regner de to steder ud med formlen for andengradsligninger:
$$ \Large x= \frac{-b \pm \sqrt{d}}{2 \cdot a} $$
Skæringspunkt 1:
$$ \large x= \frac{-(-2) + \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2+2}{4} $$
$$ \large \underline{\underline{x= 1}} $$
Skæringspunkt 2:
$$ \large x= \frac{-(-2) - \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2-2}{4} $$
$$ \large \underline{\underline{x= 0}} $$
Eksempel toppunktet
I eksemplet fandt vi ud af at diskriminanten er 4
Nu kan vi regne \((x,y)\) for toppunktet:
$$ \large x=\frac{-b}{2a} \Leftrightarrow $$
$$ \large x=\frac{-(-2)}{2\cdot 2} \Leftrightarrow $$
$$ \large x=0,5 $$
$$ \large y=\frac{-D}{4a} \Leftrightarrow $$
$$ \large y=\frac{-4}{4 \cdot 2} \Leftrightarrow $$
$$ \large y=-0,5 $$
Toppunkt = \((0,5, -0,5)\)
Koordinatsæt
Vi har nu tre koordinatsæt, de to skæringspunkter og toppunktet:
$$ \large (0,0), (0,5, -0,5), (0,1) $$
Man kunne godt tegne parablen med de tre, men jeg synes lige vi finder to mere, ved at sætte -1 og 2 ind i funktionen:
$$ \large y=2 \cdot -1^2-2 \cdot -1+0 $$
$$ \large y=4 $$
$$ \large y=2 \cdot 2^2-2 \cdot 2+0 $$
$$ \large y=4 $$
| \(x\) | 0 | 0,5 | 0 | -1 | 2 |
| \(y\) | 0 | -0,5 | 1 | 4 | 4 |
Nu kan den tegnes.