Kubisk funktion

En kubisk funktion er en funktion af tredje grad. Den generelle forskrift ser sådan ud:

$$ \large f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d $$

Her gælder at $ \large a \neq 0$, ellers ville der blive ganget med 0, og funktionen ville blive en kvadratisk funktion.

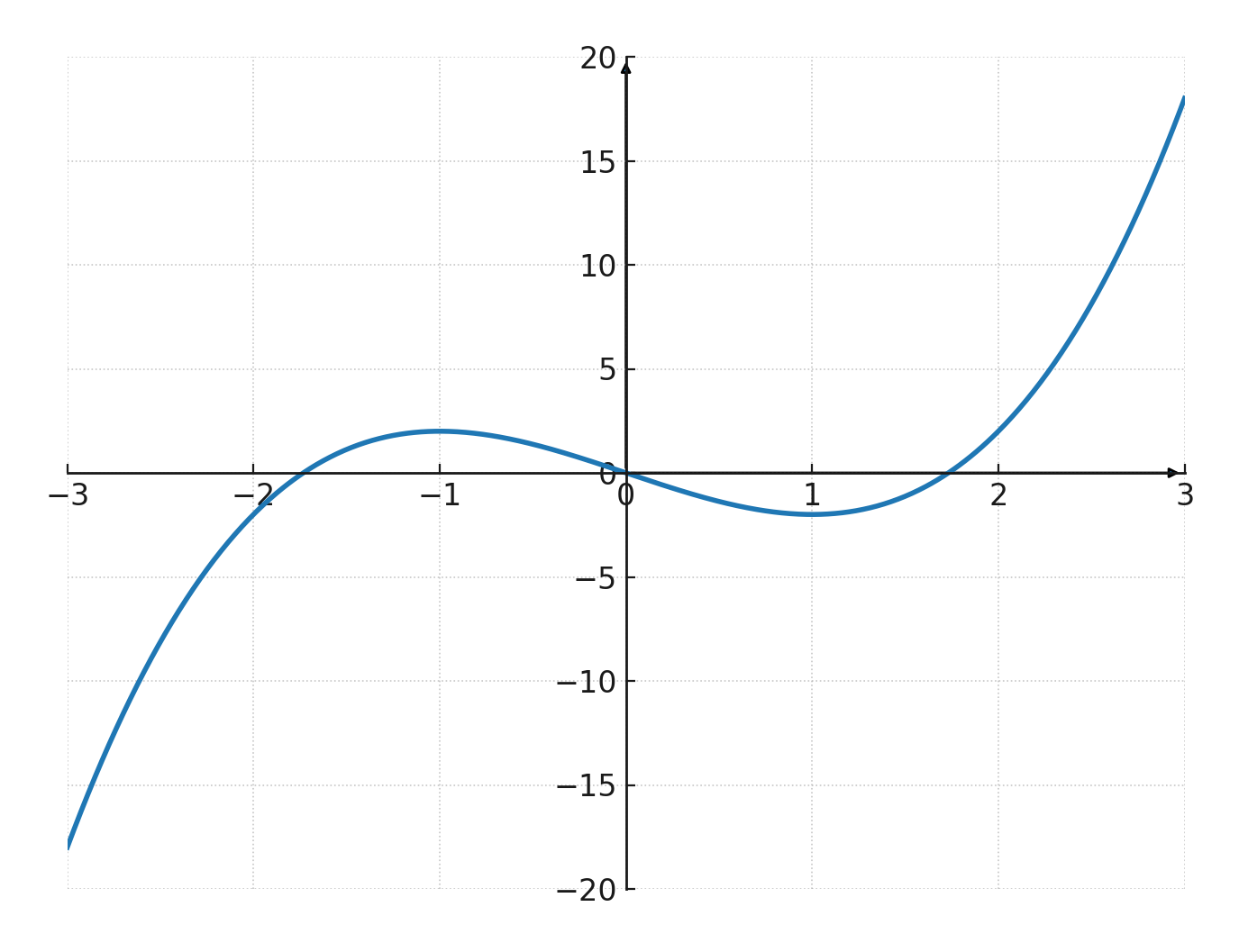
Grafen for en kubisk funktion kaldes en kubisk kurve. Den har typisk en S-form, men kan variere afhængigt af koefficienterne.

Hvis $ \large a > 0$, vil grafen starte i nederste venstre hjørne og slutte i øverste højre hjørne.
Hvis $ \large a < 0$, vil grafen starte i øverste venstre hjørne og slutte i nederste højre hjørne.

Kubisk funktion

Rødder

En kubisk funktion kan have ét eller tre skæringspunkter med x-aksen, afhængigt af diskriminanten.

En rod er det sted den enten skærer eller tangerer x-aksen, altså hvor $ \large f(x) = 0 $. Dermed har den altid mindst én reel rod og kan have op til tre reelle rødder.

Top- og bundpunkter

En kubisk funktion kan have både et lokalt maksimum (top-punkt) og et lokalt minimum (bund-punkt), hvis diskriminanten tillader det. I det tilfælde får grafen sin karakteristiske S-form.

Hvis betingelserne ikke er opfyldt, vil grafen bare stige eller falde hele vejen uden at bøje.

Andre vigtige punkter

Grafen skærer y-aksen i punktet $ \large (0,d)$
Grafen har altid et vendepunkt (inflektionspunkt) ved $ \large x=-\frac{b}{3a}$
Man kan afgøre, hvordan grafen ser ud, ud fra udtrykket $ \large b^2 - 3ac $
- Hvis $ \large b^2-3ac>0$, er der to ekstrema (et top- og et bundpunkt).
- Hvis $ \large b^2-3ac=0$, er der ét dobbelt stationært punkt.
- Hvis $ \large b^2-3ac<0$, er der ingen ekstrema.

Eksempel

Vi prøver med denne funktion:

$$ \large f(x) = x^3 - 3x + 2 $$

Her gælder at $ \large a = 1$, $ \large b = 0$, $ \large c = -3$, $ \large d = 2$.

Funktionen giver følgende koordinatsæt:

$ x $	-2	-1	0	1	2	3
$ y $	-4	4	2	0	4	20

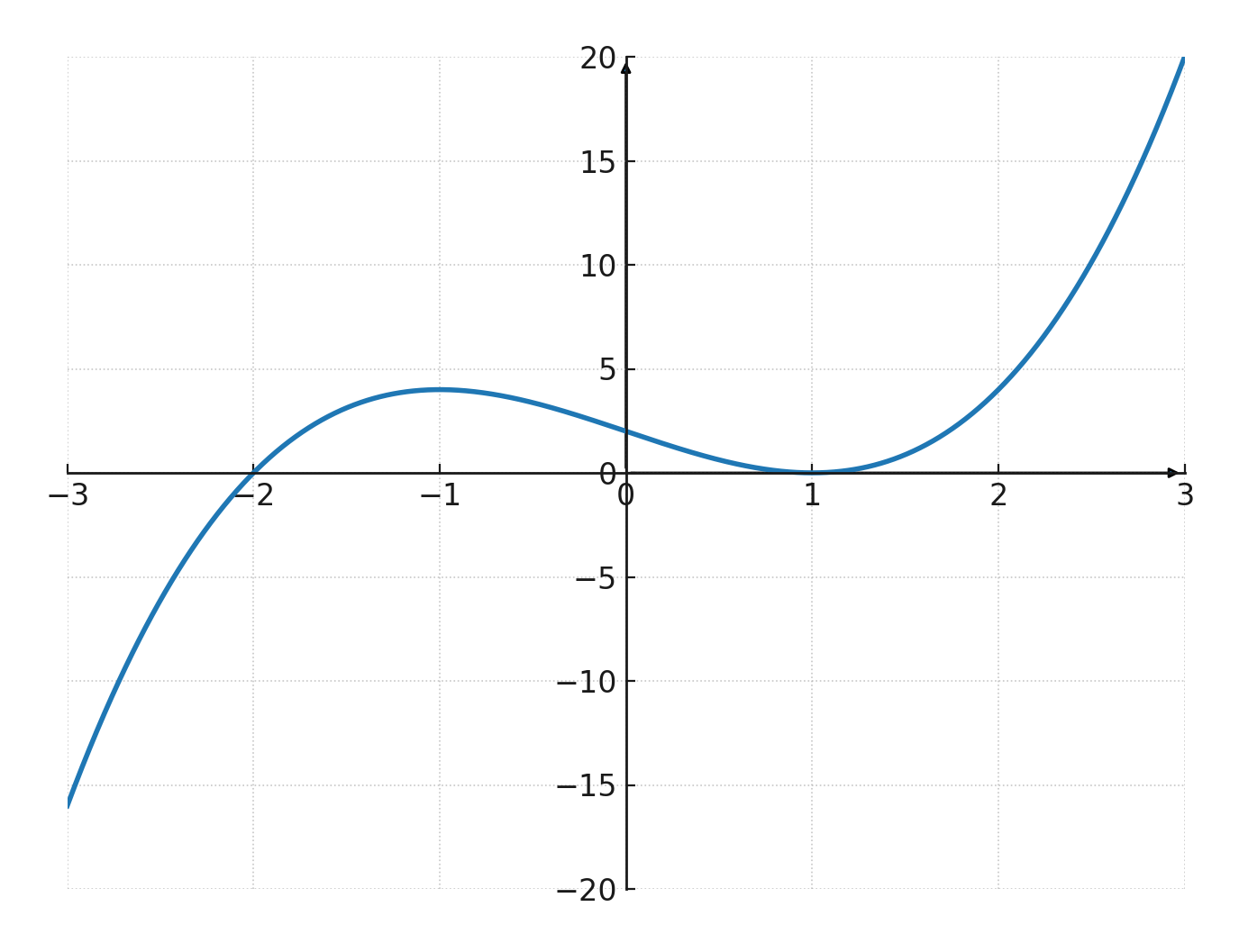
Kubisk funktion eksempel

Det er muligt at faktorisere funktionen:

$$ \large f(x) = (x+2)(x-1)^2 $$

Dermed har grafen rødderne $ \large (-2,0)$ og $ \large (1,0)$. Punktet $ \large (1,0)$ er en dobbeltrod, hvilket betyder at grafen tangerer x-aksen her uden at skære igennem.

Hvis den i stedet havde skåret igennem dette punkt, ville funktionen have haft tre forskellige rødder.

Grafen skærer y-aksen i punktet $ \large (0,2)$.

Diskriminanten giver $ \large b^2 - 3ac = 0^2 - 3 \cdot 1 \cdot (-3) = 9 > 0$, så funktionen har både et lokalt maksimum og et lokalt minimum. Derfor får grafen den klassiske S-form.