Quadratzahlen

Eine Quadratzahl ist das Ergebnis, wenn man eine Zahl zum Quadrat erhebt.

Mit anderen Worten, eine Quadratzahl hat die Form \(\large n^2\), wobei \(n\) eine Natürliche Zahl ist.

 

Beispiel

\(\large 3^2 = 9,\quad 6^2 = 36,\quad 10^2 = 100\)

 

Wenn man die Quadratwurzel von \(X\) zieht und das Ergebnis eine Ganze Zahl ist, dann ist \(X\) eine Quadratzahl. Zum Beispiel \(\large \sqrt{81} = 9\).

 

Geometrische Bedeutung

Eine Quadratzahl kann als Fläche eines Quadrats mit der Seitenlänge \(n\) gesehen werden. Zum Beispiel ist 16 die Fläche eines Quadrats mit der Seitenlänge 4.

 

\(\large \sqrt{16} = 4\)

 

Parabel im Koordinatensystem

Die Punkte \((n, n^2)\) bilden den Graphen der Funktion \(\large y = x^2\), der eine Parabel ist.

 

 

 

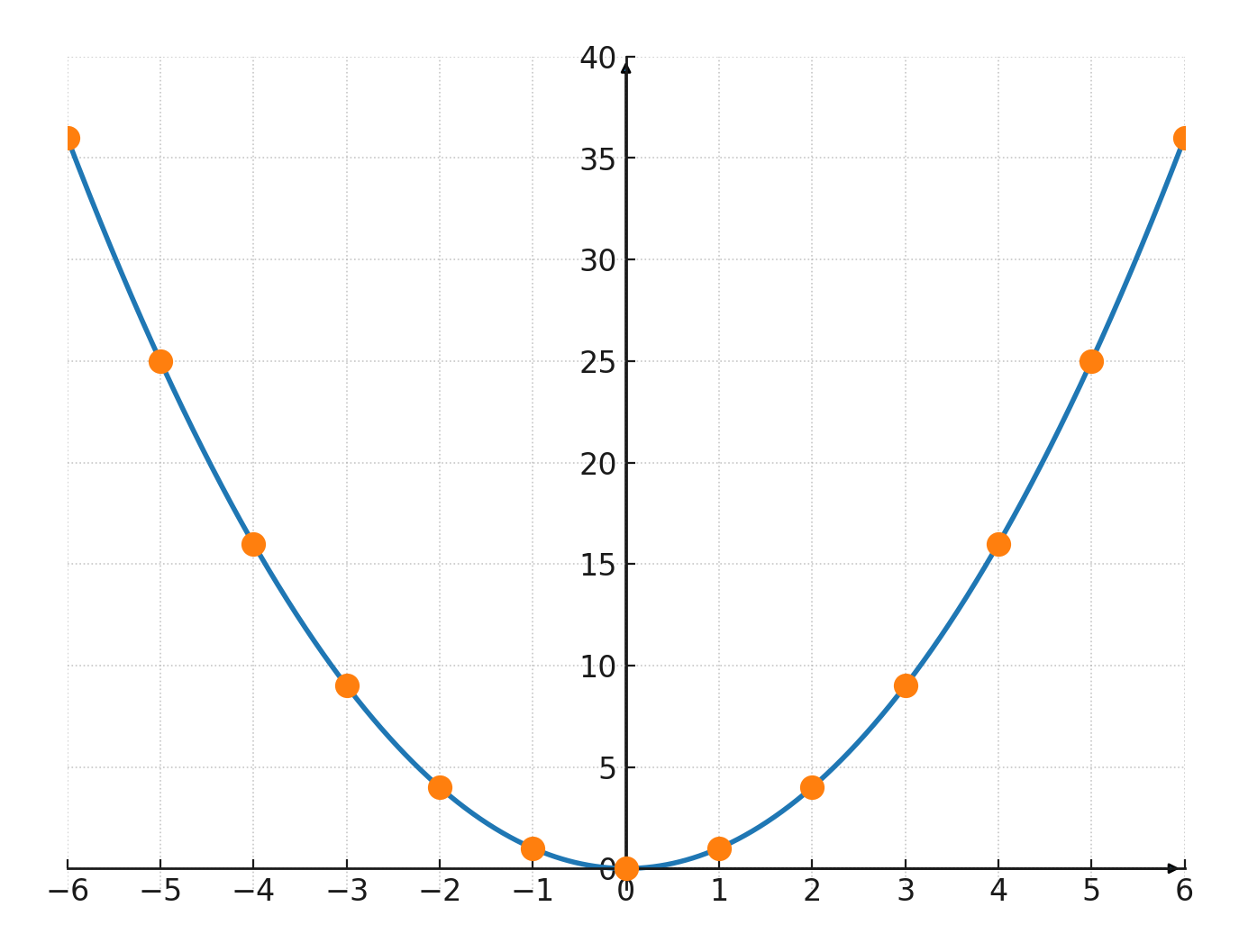
Tabelle der ersten Quadratzahlen

 

Zahl (Wurzel)	1	2	3	4	5	6	7	8	9	10
Quadratzahl	1	4	9	16	25	36	49	64	81	100

 

 

Muster in Quadratzahlen

Differenz zwischen zwei aufeinanderfolgenden Quadratzahlen:

 

\(\large (n+1)^2 - n^2 = 2n + 1\). Die Differenz ist immer eine Ungerade Zahl.

 

Summe der ersten \(n\) Ungeraden Zahlen:

 

\(\large 1 + 3 + 5 + \cdots + (2n-1) = n^2\).

 

Letzte Ziffer:

 

Eine Quadratzahl endet immer auf 0, 1, 4, 5, 6 oder 9.

 

Modulo 3:

 

Eine Quadratzahl ist entweder durch 3 teilbar oder eins mehr als ein Vielfaches von 3.

 

 

Quadratzahlen und Primfaktoren

Eine Zahl ist genau dann eine Quadratzahl, wenn alle Exponenten in ihrer Primfaktorzerlegung gerade Zahlen sind.

 

Zum Beispiel \(\large 900 = 2^2 \cdot 3^2 \cdot 5^2 = (2\cdot 3\cdot 5)^2\).

 

 

Verbindungen zu anderen Themen

Pythagoras:

 

Quadratzahlen erscheinen im Satz des Pythagoras \(\large a^2 + b^2 = c^2\).

 

Differenz von Quadraten:

 

\(\large a^2 - b^2 = (a-b)(a+b)\).