Fibonacci-Zahlen
Die Fibonacci-Zahlen sind nach Leonardo Fibonacci benannt, einem italienischen Mathematiker, der diese Zahlenfolge erstmals im Jahr 1202 im Buch Liber Abaci beschrieb.
Rekursive Definition
Die Fibonacci-Zahlen werden durch eine rekursive Funktion definiert:
$$ F_0 = 0, \quad F_1 = 1 $$
$$ F_n = F_{n-1} + F_{n-2} \quad (n \geq 2) $$
Das bedeutet, dass jede Zahl in der Folge die Summe der beiden vorhergehenden ist.
Die ersten 10 Fibonacci-Zahlen sind daher:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 $$
Man erkennt schnell das Muster:
$$ 0+1=1,\;\;1+1=2,\;\;1+2=3,\;\;2+3=5,\;\;3+5=8\;\;usw. $$
Die Fibonacci-Zahlen können durch Quadrate dargestellt werden, deren Seitenlänge den Zahlen entspricht.
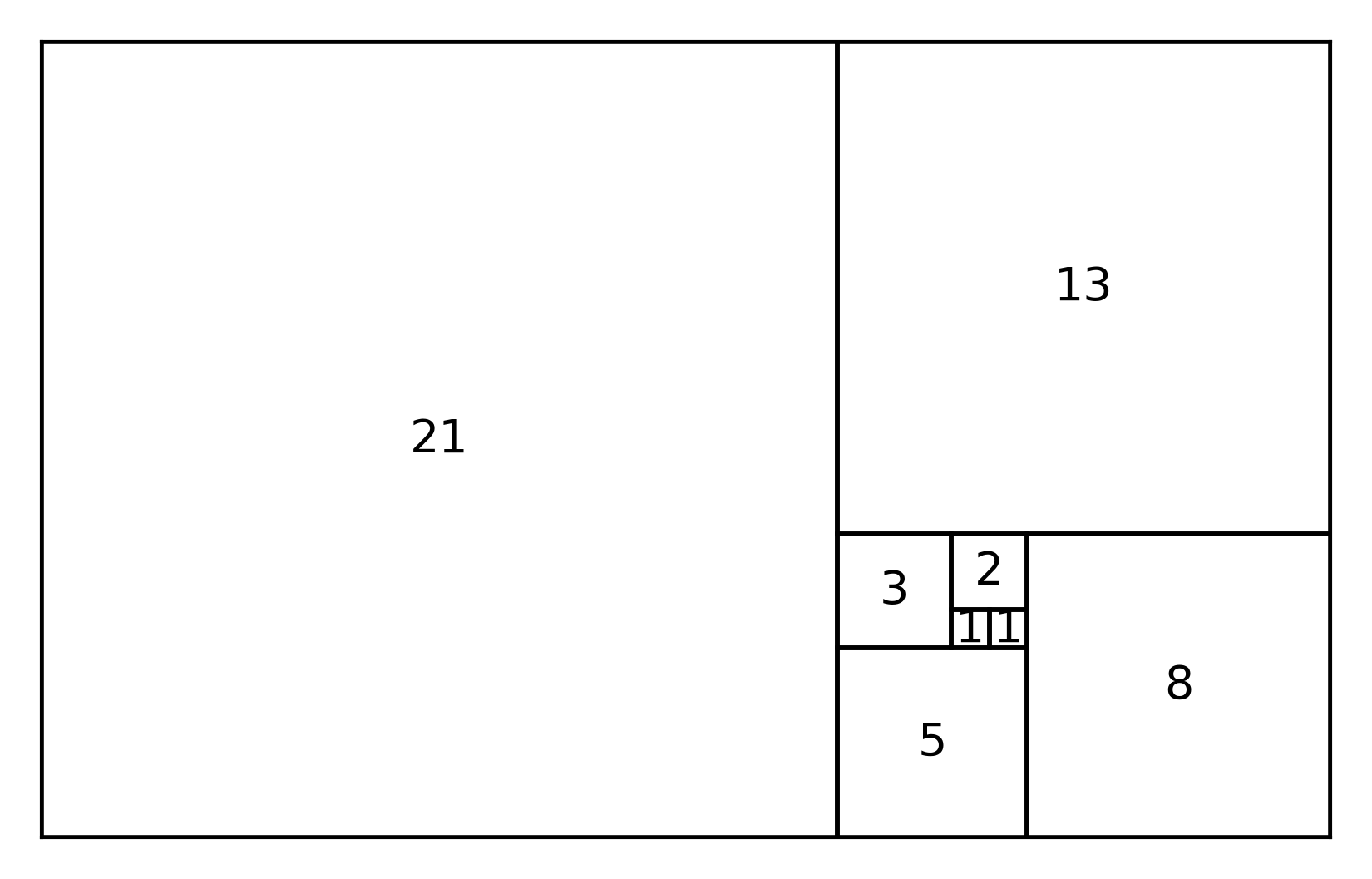
Das Verhältnis der Fibonacci-Zahlen
Nimmt man das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen, nähert sich das Ergebnis einer Konstanten, die Goldener Schnitt \(\phi\) genannt wird:
$$ \phi = \frac{1+\sqrt{5}}{2} \approx 1,618... $$
Beispiel: $$ \frac{55}{34} \approx 1,6176 $$ Je größer die Zahlen, desto näher kommt man an \(\phi\) heran.
Binetsche Formel
Es gibt eine explizite Formel (die sogenannte Binetsche Formel), mit der man eine Fibonacci-Zahl berechnen kann, ohne die vorhergehenden zu kennen:
$$ F_n = \frac{1}{\sqrt{5}}\Biggl(\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Biggr) $$
Mit der Binetschen Formel können wir berechnen:
$$ F_{25} = 75025 $$
Die 25. Fibonacci-Zahl ist also 75025.
Die Fibonacci-Spirale
Wenn man die Fibonacci-Quadrate zeichnet, kann man eine Spirale vom Zentrum nach außen ziehen. Diese Spirale findet sich in vielen natürlichen Mustern: Sonnenblumenkerne, Schneckenhäuser, Blumenkohl.

Es gibt viele Orte, an denen wir die Fibonacci-Zahlen und die Spirale im Alltag sehen und verwenden:
- Natur – Pflanzenwachstum, Blütenmuster, Samen und Schalen.
- Kunst und Architektur – Proportionen und Kompositionen basierend auf Fibonacci und dem Goldenen Schnitt.
- Informatik – Algorithmen, Datenstrukturen (Fibonacci-Heap) und effiziente Suche.
- Musik – einige Komponisten haben Fibonacci-Zahlen zur Strukturierung von Rhythmen und Takten verwendet.
Muster in den Fibonacci-Zahlen
Die Summe der ersten \(n\) Fibonacci-Zahlen:
Die Summe ist immer eins weniger als die \((n+2)\)-te Fibonacci-Zahl:
$$ F_1 + F_2 + \cdots + F_n = F_{n+2} - 1 $$
Beispiel:
Die ersten 5 Fibonacci-Zahlen sind \(1,1,2,3,5\). Die Summe ist:
$$ 1+1+2+3+5 = 12 $$
Die 7. Fibonacci-Zahl ist 13, und \(13-1=12\). Die Regel stimmt.
Die Summe der Quadrate der Fibonacci-Zahlen:
Die Summe der Quadrate bis \(F_n\) ist gleich dem Produkt von \(F_n\) und \(F_{n+1}\):
$$ F_1^2 + F_2^2 + \cdots + F_n^2 = F_n \cdot F_{n+1} $$
Beispiel 1:
Für \(n=3\):
$$ 1^2+1^2+2^2+3^2 = 15 $$
Und gleichzeitig:
$$ 3 \cdot 5 = 15 $$
Beispiel 2:
Für \(n=5\):
$$ 1^2+1^2+2^2+3^2+5^2 = 40 $$
Und:
$$ 5 \cdot 8 = 40 $$
Die Regel gilt für alle Fibonacci-Zahlen.
Weitere Muster:
- Jede zweite Fibonacci-Zahl ist gerade.
- Jede dritte ist durch 2 teilbar, jede vierte durch 3 usw.
- Die Fibonacci-Zahlen können als Diagonalsummen im Pascalschen Dreieck gefunden werden.
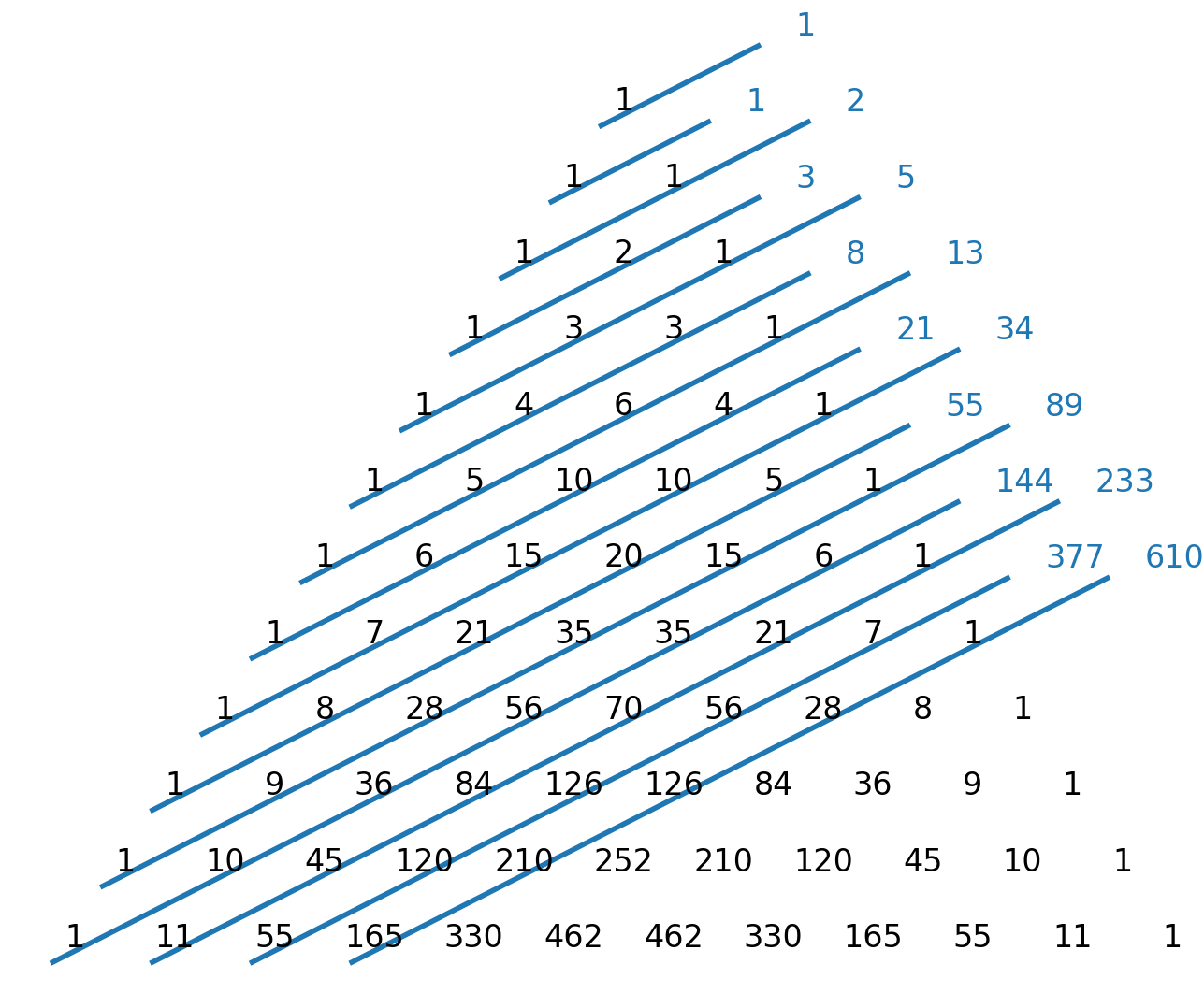
Zusammenfassung
Die Fibonacci-Folge beginnt einfach: \(0, 1, 1, 2, 3, 5...\), enthält aber tiefe Muster und Verbindungen zu Natur, Kunst und Mathematik.
Von rekursiven Definitionen bis zur Binetschen Formel und dem Goldenen Schnitt – die Fibonacci-Zahlen sind sowohl schön als auch nützlich.