Zahlen

Zahlen sind ein weites Konzept, das grundlegend verwendet wird, um eine Menge oder eine Größe anzugeben.

Es gibt viele verschiedene Arten von Zahlen, die in Kategorien eingeteilt sind. In der Mathematik arbeiten wir mit allen, und sie können als verschachtelte Mengen gesehen werden, wobei jede neue Kategorie die vorherige erweitert.

Im Folgenden findet sich eine kurze Beschreibung der wichtigsten Kategorien.

 

Natürliche Zahlen \(\ N\)

Die Natürlichen Zahlen sind alle ganzen Zahlen größer als null: 1, 2, 3, 4, 5, 6 … usw. Sie werden mit \(\large N\) bezeichnet. In manchen Zusammenhängen wird auch die 0 eingeschlossen, und dann schreibt man \(\large N_0\).

 

Ganze Zahlen \(\ Z\)

Wenn wir die Natürlichen Zahlen (einschließlich 0) um die negativen Zahlen erweitern, erhalten wir die Ganzen Zahlen:

… -4, -3, -2, -1, 0, 1, 2, 3 … usw.

Sie werden mit \(\large Z\) bezeichnet.

 

Rationale Zahlen \(\ Q\)

Die Rationalen Zahlen sind alle Zahlen, die als Bruch geschrieben werden können, wobei der Zähler eine Ganze Zahl und der Nenner eine Natürliche Zahl ungleich 0 ist. Beispiele:

 

\(\large \frac{1}{4} = 0,25\), \(\large -\frac{3}{5} = -0,6\)

 

Auch alle endlichen und periodischen Dezimalbrüche gehören hierher.

Sie werden mit \(\large Q\) bezeichnet.

 

Reelle Zahlen \(\ R\)

Die Reellen Zahlen umfassen alle zuvor genannten Mengen von Zahlen, aber auch die Irrationalen Zahlen, die nicht als Brüche geschrieben werden können. Irrationale Zahlen haben eine unendliche nicht periodische Dezimalentwicklung.

Beispiele sind \(\large \pi\) und \(\large \sqrt{5}\).

 

\(\large \sqrt{5} \) ist eine Reelle Zahl, aber zugleich eine Irrationale Zahl, da sie nicht als Bruch geschrieben werden kann.

Die Reellen Zahlen werden mit \(\large R\) bezeichnet.

 

Komplexe Zahlen \(\ C\)

Die Komplexen Zahlen erweitern die Reellen Zahlen durch die Aufnahme der Imaginären Zahlen. Während eine Reelle Zahl auf einer Zahlengeraden dargestellt werden kann, kann eine Komplexe Zahl in der Ebene als Punkt mit den Koordinaten \(\large (x,y)\) dargestellt werden, wobei \(x\) der Reelle Teil und \(\large y\) der Imaginäre Teil ist. Eine Komplexe Zahl wird in der Form geschrieben:

 

\(\large z = x + yi \)

 

Hier ist \(i\) die Imaginäre Einheit, definiert durch \(\large i^2 = -1\). Ein Beispiel ist:

 

\(\large z = 3 + 2i \)

 

Dies kann als der Punkt \(\large (3,2)\) in der Komplexen Ebene verstanden werden.

Komplexe Zahlen werden zum Beispiel verwendet, um Gleichungen zu lösen, die keine Reellen Lösungen haben, wie:

 

\(\large x^2 + 1 = 0 \implies x = \pm i \)

 

Die Komplexen Zahlen werden mit \(\large C\) bezeichnet.

 

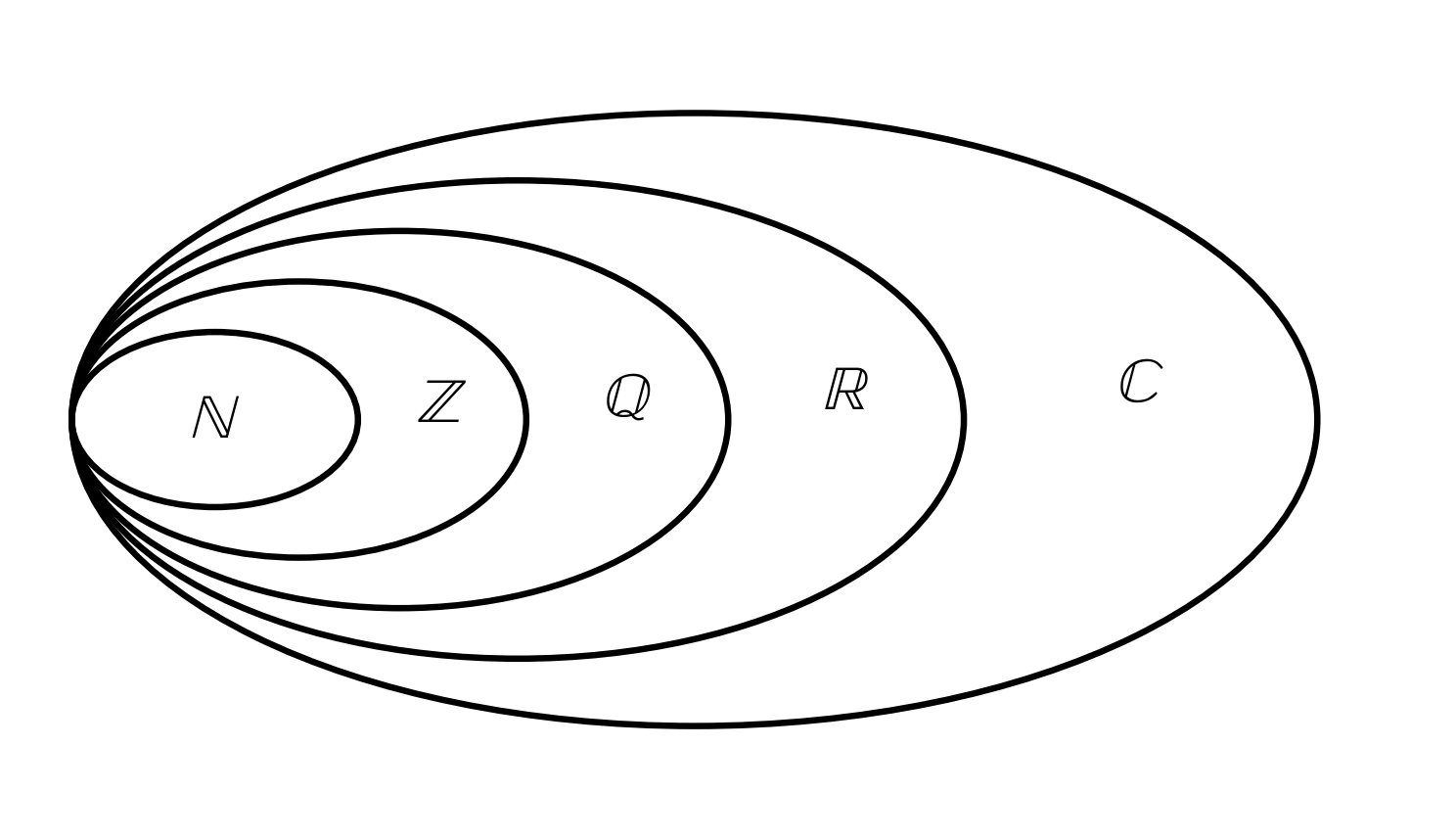
Das Bild zeigt die Natürlichen Zahlen als Teil der Ganzen Zahlen, die wiederum Teil der Rationalen Zahlen sind, usw.

 

Zusammenfassung

Die Hierarchie der Zahlmengen kann kurz so geschrieben werden:

 

\(\Large N \subset Z \subset Q \subset R \subset C\)