Système de coordonnées

Un système de coordonnées est constitué de deux droites numériques qui sont perpendiculaires l’une à l’autre. Les droites numériques sont appelées axes.

L’axe horizontal est appelé axe des x ou premier axe, et l’axe vertical est appelé axe des y ou deuxième axe.

Les deux axes se coupent en leur point zéro. Ce point est appelé origine.

 

 

Points dans le système de coordonnées

Un point dans le système de coordonnées peut être lu en suivant une ligne perpendiculaire aux axes et en lisant la valeur de l’axe des x et celle de l’axe des y à cet endroit. L’axe des x est toujours lu en premier, donc un point s’écrit \( \large (x,y)\).

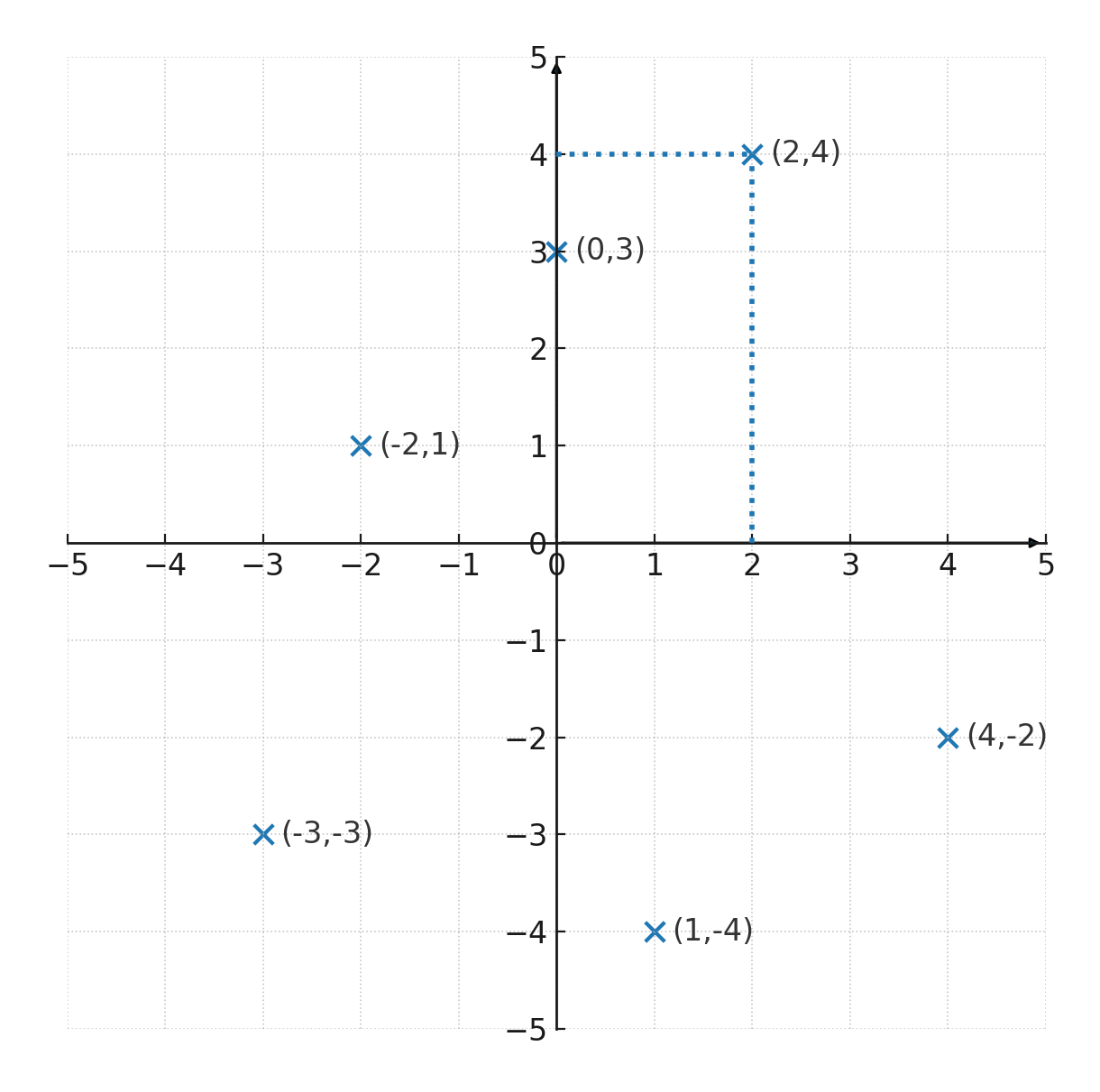
Dans le système de coordonnées ci-dessous, différents points sont représentés.

Le point \( \large (2,4)\) se trouve dans le système de coordonnées, où les deux lignes perpendiculaires montrent que :

• axe des x = 2
• axe des y = 4

 

 

 

Quadrants

Les quatre zones du système de coordonnées sont appelées quadrants, où :

 

• 1er quadrant : \( \large (x,y)\)
• 2e quadrant : \( \large (-x,y)\)
• 3e quadrant : \( \large (-x,-y)\)
• 4e quadrant : \( \large (x,-y)\)

 

Trois dimensions

Le système de coordonnées peut également être étendu à trois dimensions en ajoutant un axe z, qui est perpendiculaire aux axes x et y à l’origine.

Dans le système bidimensionnel, il y a quatre quadrants, mais dans le système tridimensionnel, l’espace est divisé en huit zones, appelées octants.

Les points sont écrits avec trois nombres \( (x,y,z) \). Cela est utilisé par exemple en géométrie de l’espace.