Fonctions rationnelles

Une fonction rationnelle est une fraction où le numérateur et le dénominateur sont des polynômes. Ainsi, une fonction rationnelle peut s’écrire comme :

 

$$ \large f(x) = \frac{P(x)}{Q(x)} $$

 

Ici, \(P(x)\) et \(Q(x)\) sont des polynômes, et le dénominateur \(Q(x)\) ne doit pas être égal à 0.

Les fonctions rationnelles peuvent avoir des asymptotes verticales là où le dénominateur devient 0, et elles peuvent avoir des asymptotes horizontales ou obliques, selon le degré du numérateur et du dénominateur.

 

Exemple de fonction rationnelle

Un exemple de fonction rationnelle est :

 

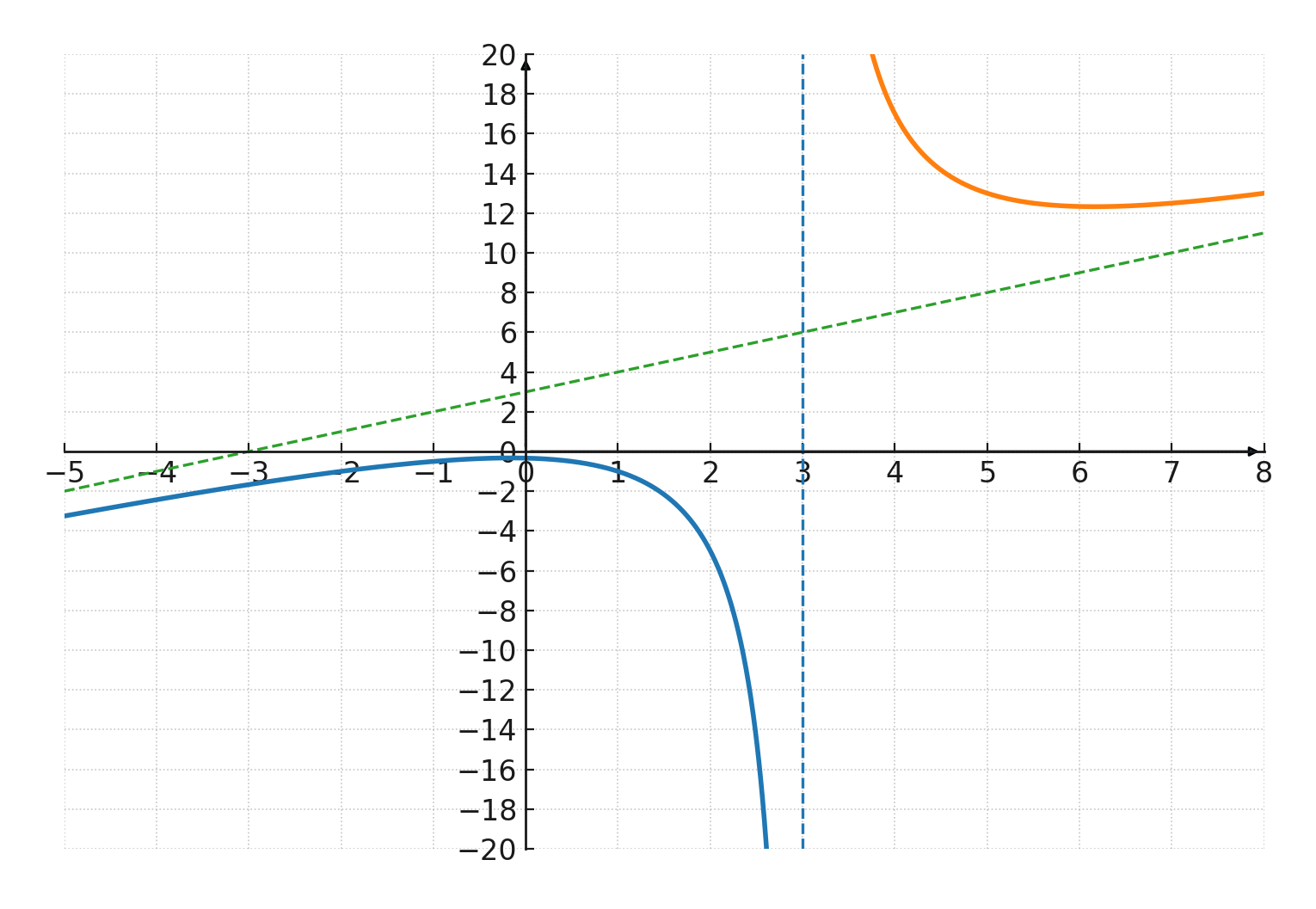
$$ \large f(x) = \frac{x^2+1}{x-3} $$

 

Dans cet exemple, le numérateur est \(x^2+1\), qui est un polynôme du 2e degré, et le dénominateur est \(x-3\), qui est un polynôme du 1er degré.

 

• La fonction n’est pas définie pour \(x=3\), car on ne peut pas diviser par 0.
• Le graphique a donc une asymptote verticale en \(x=3\).
• Quand \(x\) devient très grand ou très petit, la fraction se comporte approximativement comme \(\tfrac{x^2}{x} = x\). Ainsi, le graphique a une asymptote oblique proche de la droite \(y=x\).

 

 

 

Proportionnalité inverse

L’un des types les plus simples de fonctions rationnelles est la fonction proportionnelle inverse :

 

$$ \large f(x) = \frac{k}{x} $$

 

Ici, \(k\) est une constante. La fonction n’est pas définie pour \(x=0\), car on ne peut pas diviser par zéro.

Le graphique a une forme caractéristique, situé dans les 1er et 3e quadrants si \(k\) est positif, et dans les 2e et 4e quadrants si \(k\) est négatif.

 

Cette fonction est appelée proportionnelle inverse car lorsque \(x\) est multiplié par deux, \(f(x)\) est réduit de moitié. Le produit \(x \cdot f(x)\) est toujours le même (égal à \(k\)).