Polynômes

Un polynôme est un type spécifique de fonction mathématique, composé de termes où une variable (généralement appelée x) est élevée à différentes puissances et multipliée par des nombres (coefficients). Enfin, plusieurs de ces termes peuvent être additionnés.

 

Le type le plus simple de polynôme est une fonction constante. On l’appelle un polynôme du 0^e degré, car il n’y a pas de x. La fonction a toujours la même valeur, quel que soit x.

Un exemple est :

 

$$ \large f(x) = 5 $$

 

Ici, la valeur est toujours 5, que x soit -10, 0 ou 100. Le graphique est donc une ligne horizontale parallèle à l’axe des abscisses.

 

Voici un exemple de polynôme du 2^e degré. On l’appelle aussi une fonction quadratique :

 

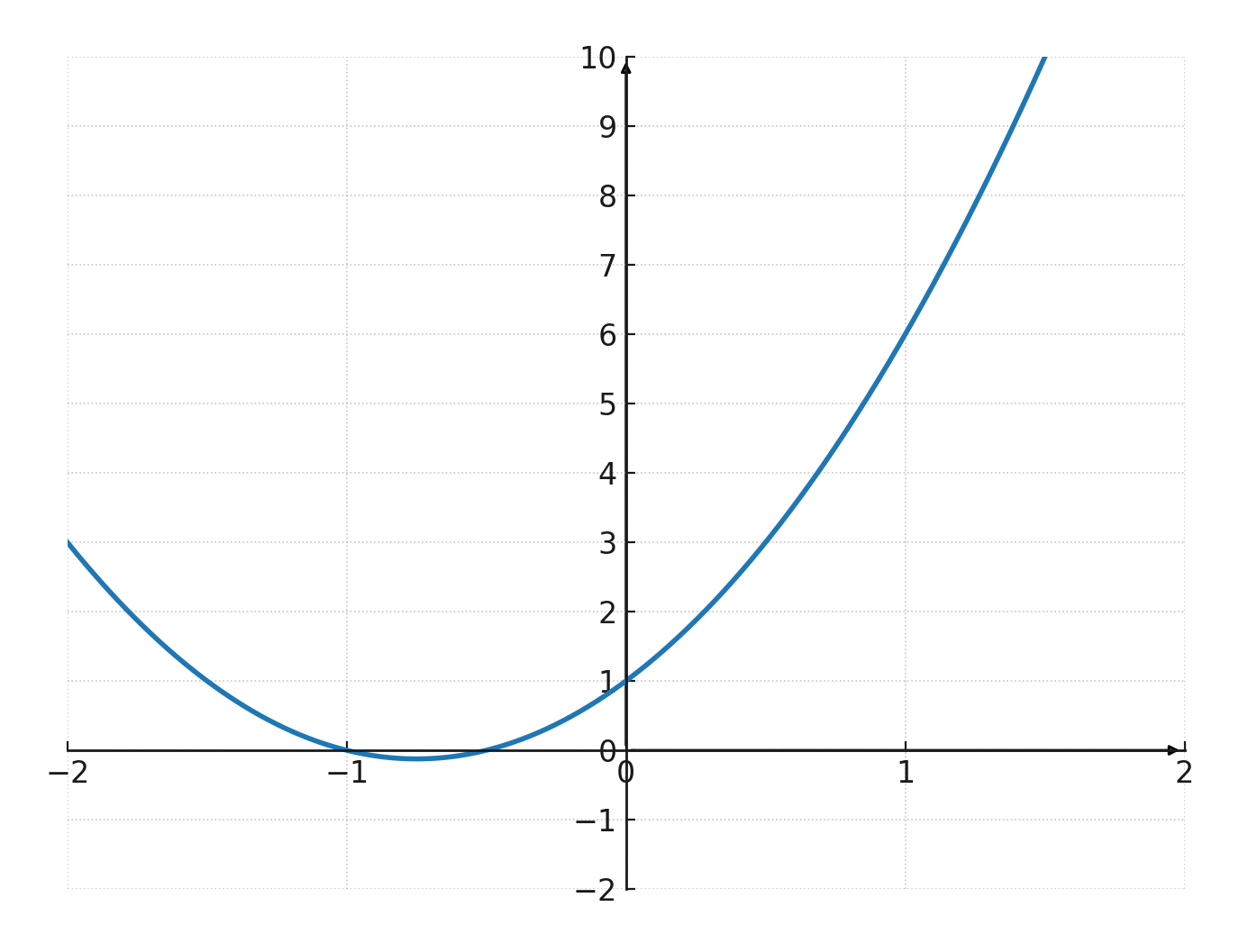
$$ \large f(x) = 2x^2 + 3x + 1 $$

 

Ici, il y a trois termes : \(2x^2\), \(3x\) et \(1\). Si on le trace sur un graphique, on obtient une parabole :

 

 

 

Le degré d’un polynôme

La puissance la plus élevée de x (l’exposant) s’appelle le degré du polynôme :

 

• 0^e degré : Fonction constante, ex. \( f(x)=5 \).
• 1^er degré : Fonction linéaire, ex. \( f(x)=2x+1 \).
• 2^e degré : Fonction quadratique, ex. \( f(x)=x^2-3x+2 \).
• 3^e degré : Fonction cubique, ex. \( f(x)=x^3-3x+2 \).

 

À partir du 4^e degré et au-delà, on utilise généralement simplement l’expression polynôme du n^e degré au lieu d’un nom particulier.

 

Plus le degré est élevé, plus les graphiques deviennent complexes et les courbes peuvent se plier de plusieurs façons.

 

Une famille infinie

Les polynômes forment toute une famille de fonctions.

Il existe des polynômes de tous degrés, et l’on peut donc dire qu’il s’agit en principe d’une suite infinie de fonctions. Chaque polynôme a son propre graphique particulier, en fonction du degré et des nombres utilisés comme coefficients.

 

Où utilise-t-on les polynômes ?

Les polynômes sont importants car ils apparaissent dans de nombreux domaines des mathématiques et de la vie réelle :

 

• En économie, une fonction peut décrire l’évolution d’un intérêt ou d’un investissement.
• En physique, une fonction peut décrire un mouvement ou une vitesse.
• En statistique, ils aident à ajuster des courbes aux données.

 

Bien que les polynômes paraissent techniques, ils sont en fait des blocs de construction fondamentaux des mathématiques, qui nous donnent des outils pour décrire et comprendre aussi bien une simple ligne droite que des relations beaucoup plus complexes.