Fonction cubique

Une fonction cubique est une fonction de troisième degré. La formule générale est la suivante :

$$ \large f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d $$

Ici, $ \large a \neq 0$, sinon il y aurait une multiplication par 0 et la fonction deviendrait une fonction quadratique.

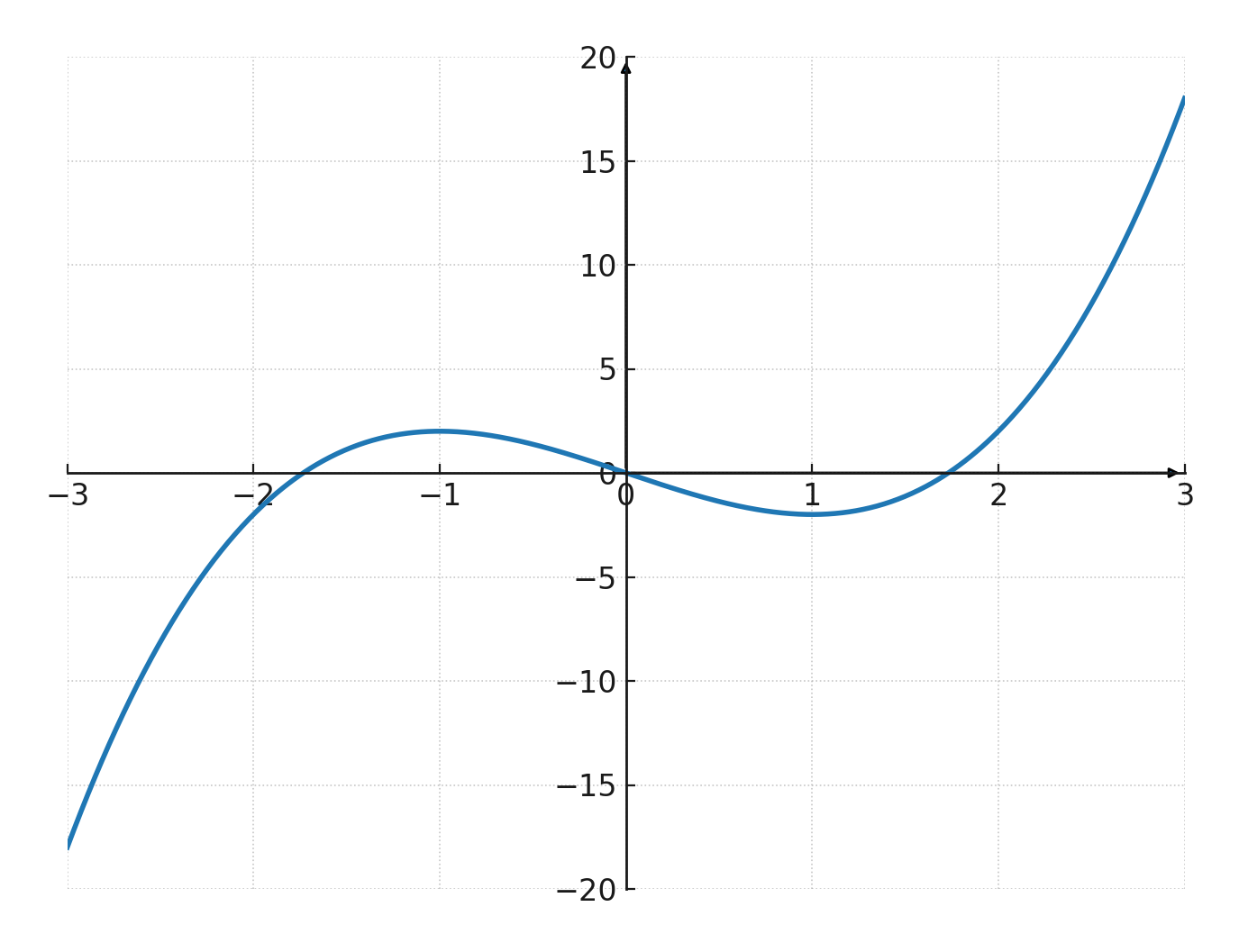
Le graphe d’une fonction cubique s’appelle une courbe cubique. Il a généralement une forme en S, mais peut varier selon les coefficients.

Si $ \large a > 0$, le graphe commence en bas à gauche et se termine en haut à droite.
Si $ \large a < 0$, le graphe commence en haut à gauche et se termine en bas à droite.

Fonction cubique

Racines

Une fonction cubique peut avoir une ou trois intersections avec l’axe des x, selon le discriminant.

Une racine est le point où elle coupe ou touche l’axe des x, c’est-à-dire où $ \large f(x) = 0 $. Elle a donc toujours au moins une racine réelle et peut en avoir jusqu’à trois.

Points maximum et minimum

Une fonction cubique peut avoir à la fois un maximum local (point haut) et un minimum local (point bas), si le discriminant le permet. Dans ce cas, le graphe prend sa forme caractéristique en S.

Si les conditions ne sont pas remplies, le graphe montera ou descendra simplement sans se courber.

Autres points importants

Le graphe coupe l’axe des y au point $ \large (0,d)$
Le graphe a toujours un point d’inflexion en $ \large x=-\frac{b}{3a}$
On peut déterminer la forme du graphe à partir de l’expression $ \large b^2 - 3ac $
- Si $ \large b^2-3ac>0$, il y a deux extrema (un maximum et un minimum).
- Si $ \large b^2-3ac=0$, il y a un point stationnaire double.
- Si $ \large b^2-3ac<0$, il n’y a pas d’extrema.

Exemple

Essayons avec cette fonction :

$$ \large f(x) = x^3 - 3x + 2 $$

Ici $ \large a = 1$, $ \large b = 0$, $ \large c = -3$, $ \large d = 2$.

La fonction donne l’ensemble de coordonnées suivant :

$ x $	-2	-1	0	1	2	3
$ y $	-4	4	2	0	4	20

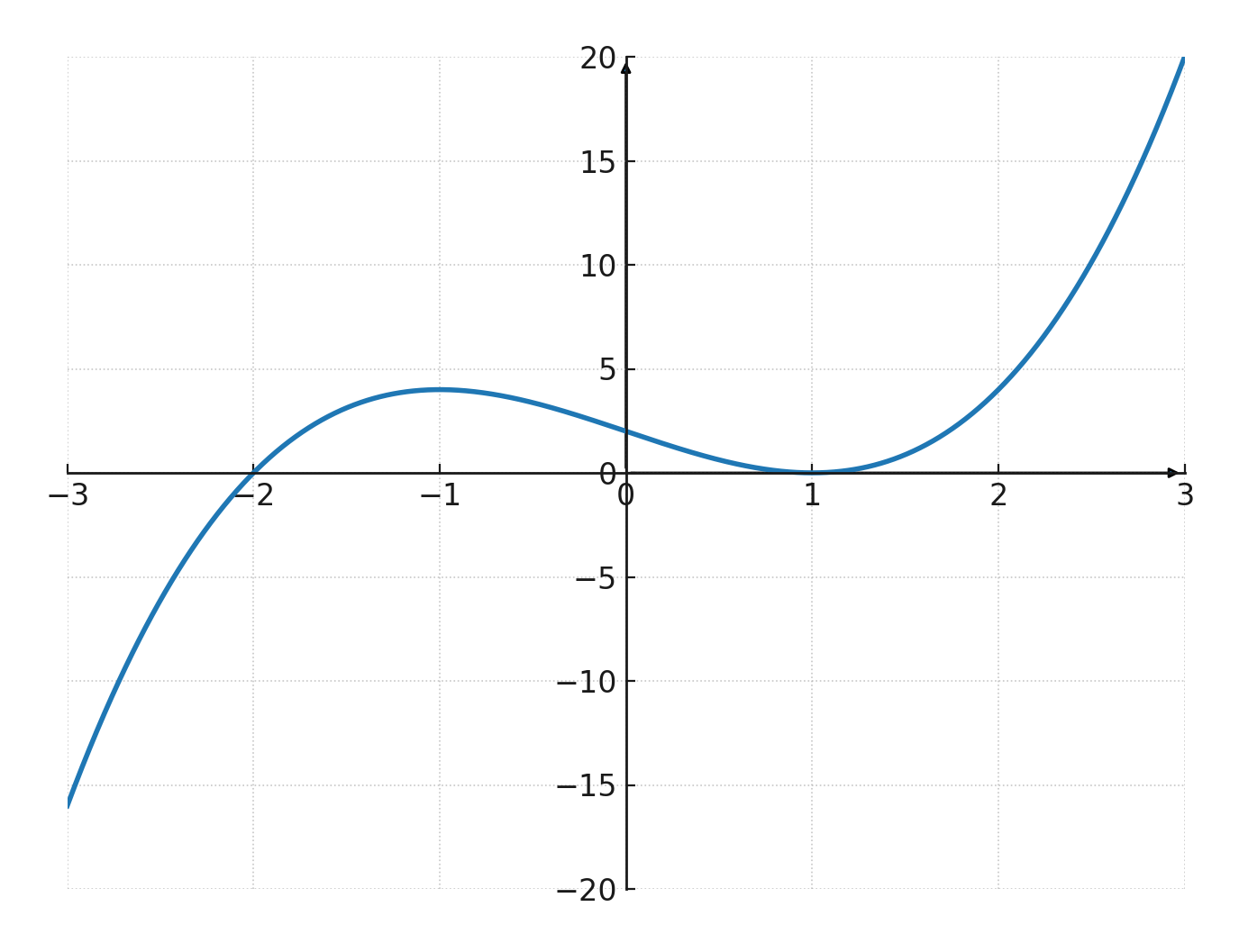
Exemple de fonction cubique

Il est possible de factoriser la fonction :

$$ \large f(x) = (x+2)(x-1)^2 $$

Ainsi, le graphe a pour racines $ \large (-2,0)$ et $ \large (1,0)$. Le point $ \large (1,0)$ est une racine double, ce qui signifie que le graphe touche l’axe des x à ce point sans le traverser.

Si au contraire il l’avait traversé, la fonction aurait eu trois racines distinctes.

Le graphe coupe l’axe des y au point $ \large (0,2)$.

Le discriminant donne $ \large b^2 - 3ac = 0^2 - 3 \cdot 1 \cdot (-3) = 9 > 0$, donc la fonction a à la fois un maximum local et un minimum local. C’est pourquoi le graphe prend la forme classique en S.