Fonctions fractionnaires
Une fonction fractionnaire est un synonyme d'une fonction rationnelle.
C’est-à-dire une fonction écrite comme:
\( \large f(x) = \frac{P(x)}{Q(x)} \)
Lorsqu’on analyse une fonction fractionnaire, on procède généralement dans cet ordre :
On détermine d’abord le domaine, puis les zéros, ensuite l’intersection avec l’axe des y et enfin les asymptotes.
Cela donne une description cohérente de la courbe.
Domaine :
Le domaine est l’ensemble de toutes les valeurs de x permises pour la fonction.
Pour une fonction fractionnaire, le domaine est l’ensemble des réels où \(\large Q(x)\neq 0 \).
Si le numérateur et le dénominateur deviennent tous deux égaux à 0 pour la même valeur de x (facteur commun), le point est quand même exclu du domaine et apparaît comme un trou dans la courbe.
Si \(\large Q(x)=0 \) mais \(\large P(x)\neq 0 \), on obtient généralement une asymptote verticale.
Zéros :
La courbe a des zéros aux points où le numérateur est nul, à condition que le dénominateur ne soit pas également nul en ce point.
Intersection avec l’axe des y :
Elle se trouve en insérant \( \large x = 0 \), si cela appartient au domaine.
Asymptotes :
Les asymptotes verticales apparaissent généralement aux valeurs de \( \large x \) où le dénominateur est nul. Les asymptotes horizontales ou obliques se trouvent en comparant les degrés du numérateur et du dénominateur ou par division polynomiale.
Un exemple est la fonction :
$$ \large f(x) = \frac{x^2 - 1}{x^2 - 4} $$
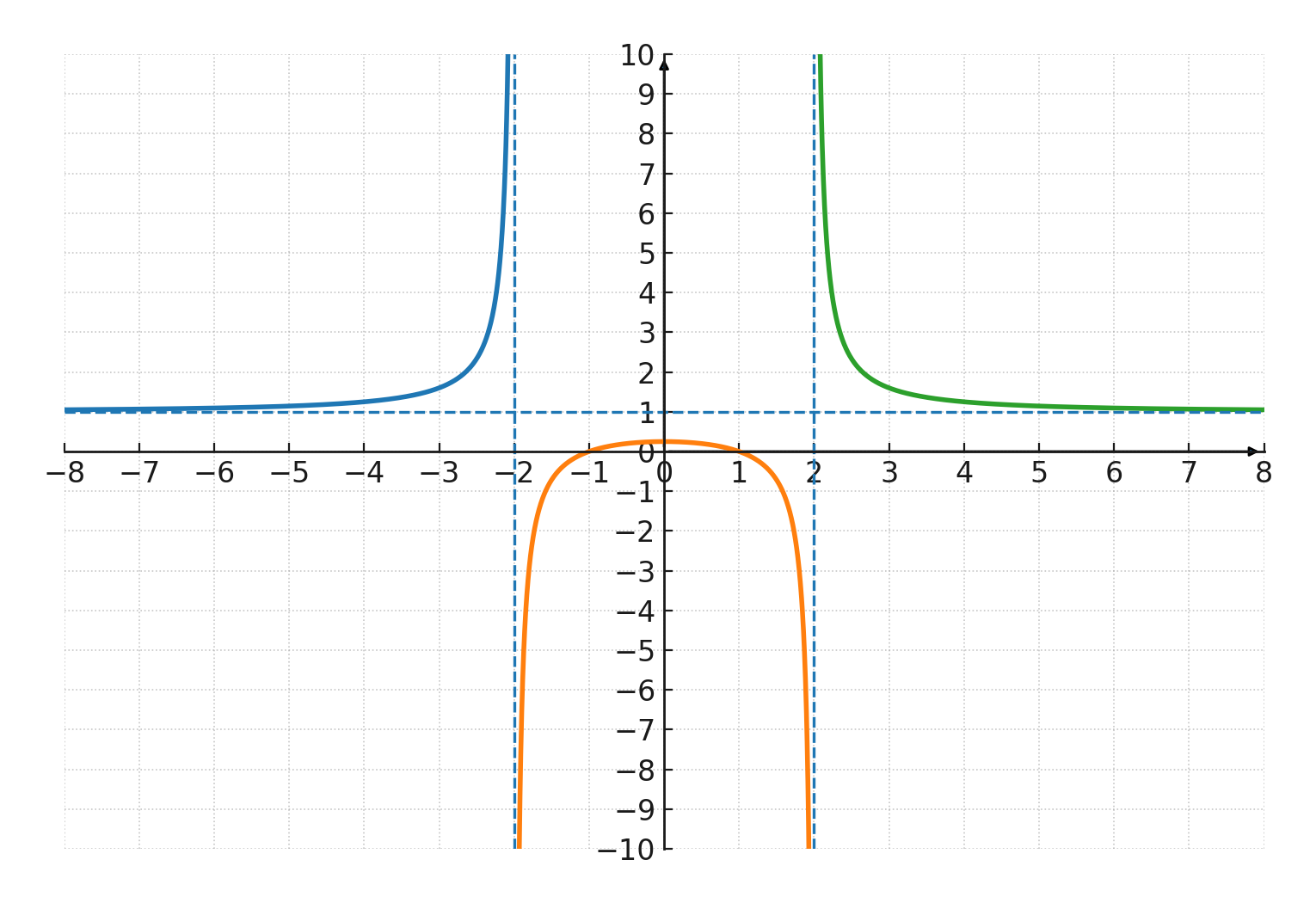
Ici le numérateur est \( \large x^2 - 1 \), ce qui donne des zéros en \( \large x = 1 \) et \( \large x = -1 \).
Le dénominateur \( \large x^2 - 4 \) devient nul en \( \large x = -2 \) et \( \large x = 2 \), donc la fonction n’est pas définie là.
Le domaine est donc tous les réels \( \large x \) sauf \( \large -2 \) et \( \large 2 \). La courbe a des asymptotes verticales en \( \large x = -2 \) et \( \large x = 2 \).
Comme le degré du numérateur et du dénominateur est le même, on obtient une asymptote horizontale en \( \large y = 1 \). L’intersection avec l’axe des y se trouve en \( \large x = 0 \) : \( \large f(0) = \frac{-1}{-4} = \frac{1}{4} \).
Avec cette méthode, on obtient une vue d’ensemble du comportement des fonctions fractionnaires.