Asymptotes

Une asymptote est une droite que la courbe d’une fonction s’approche de plus en plus, sans jamais la couper (ou seulement en quelques points isolés). Pour les fonctions rationnelles, les asymptotes sont très courantes.

 

Il existe trois types d’asymptotes :

 

Asymptotes verticales :

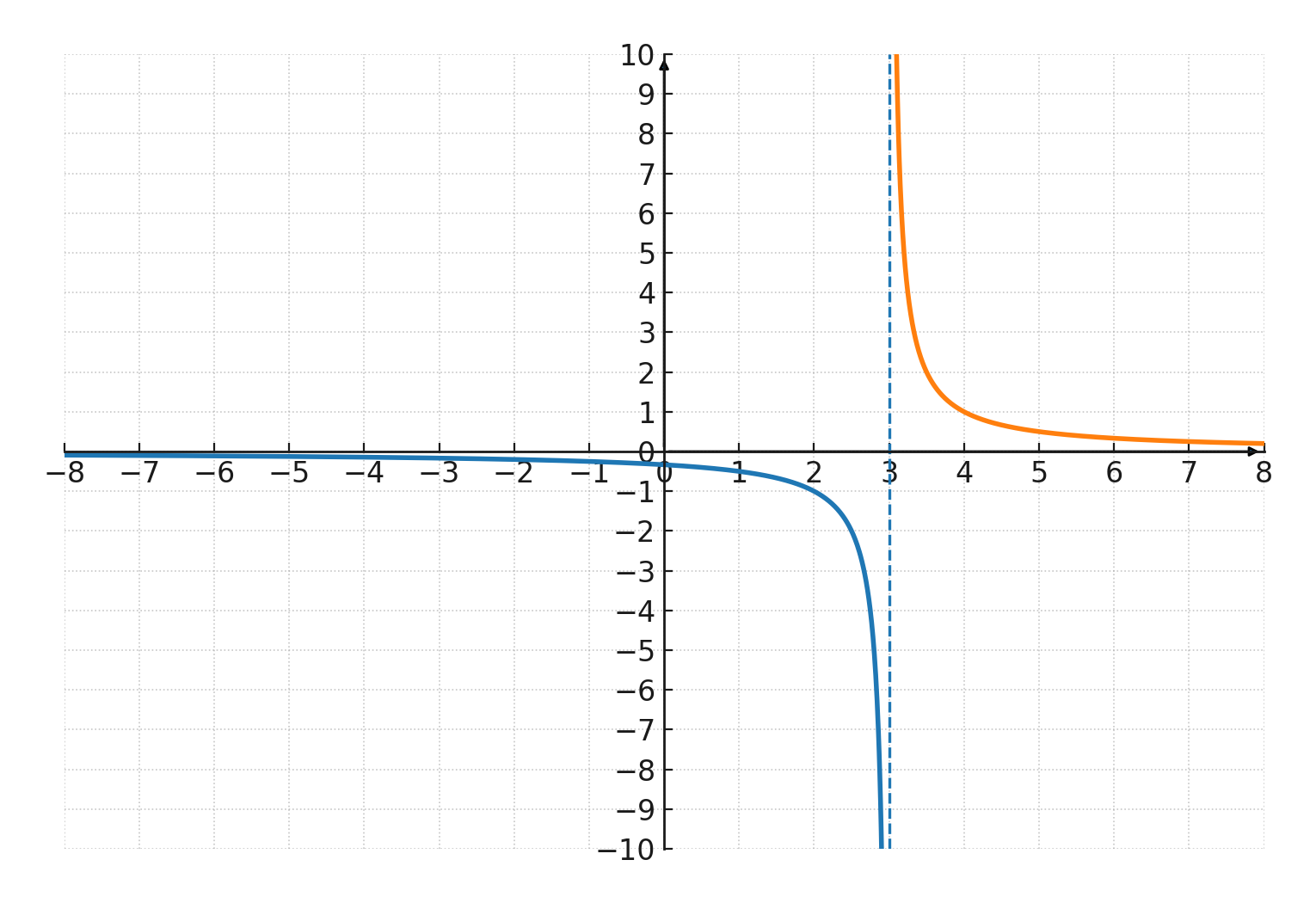
Elles apparaissent lorsque le dénominateur d’une fonction rationnelle devient nul. Par exemple, la fonction \( \Large f(x) = \frac{1}{x-3} \) a une asymptote verticale en \(\large x = 3 \).

La fonction a également l’axe des abscisses comme asymptote horizontale.

 

Asymptotes horizontales :

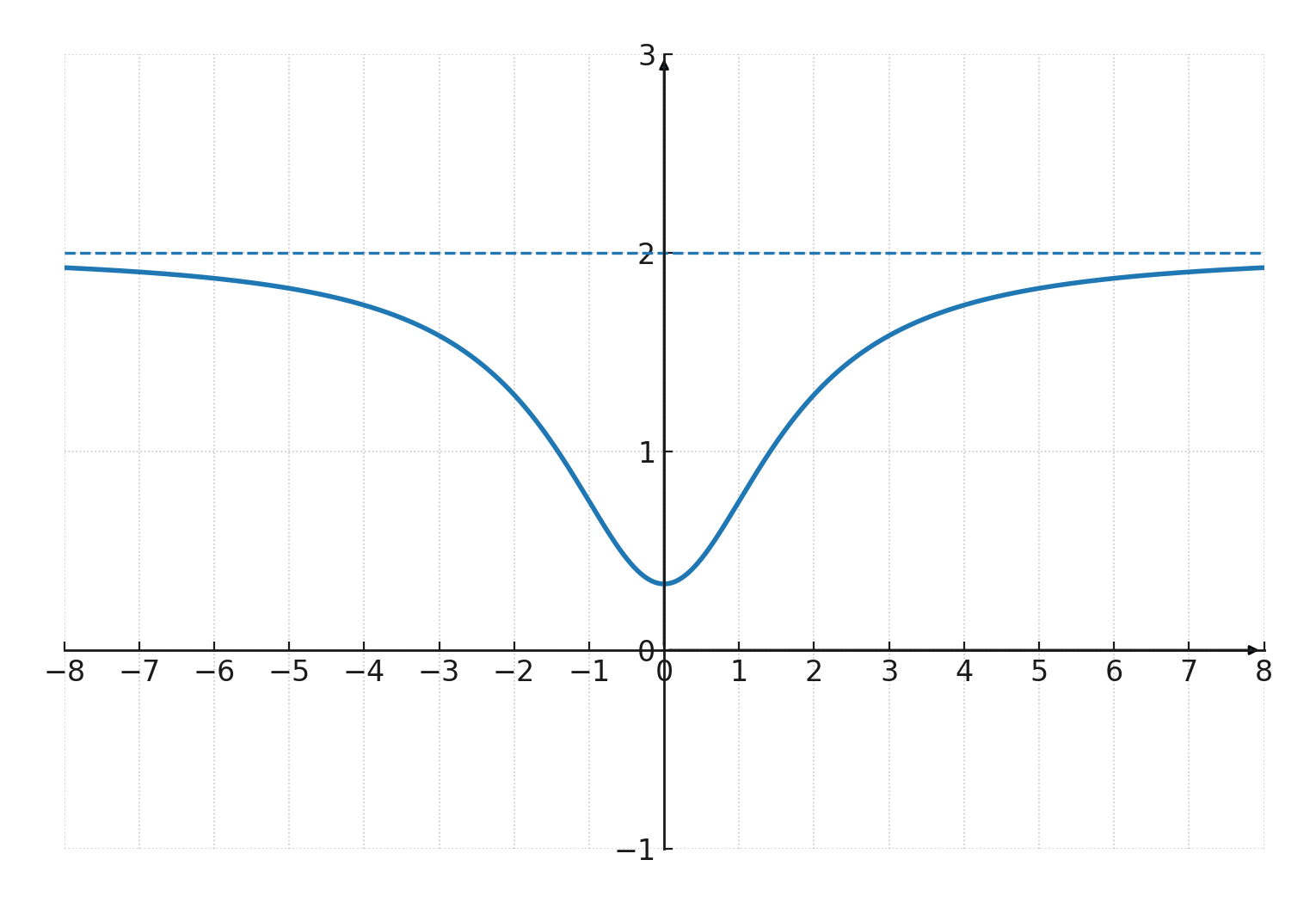
Elles apparaissent lorsque la courbe d’une fonction tend vers une valeur constante lorsque \(\large x \) devient très grand ou très petit.

Par exemple, \(\Large f(x) = \frac{2x^2+1}{x^2+3} \) a une asymptote horizontale en \(\large y = 2 \).

 

 

Asymptotes obliques :

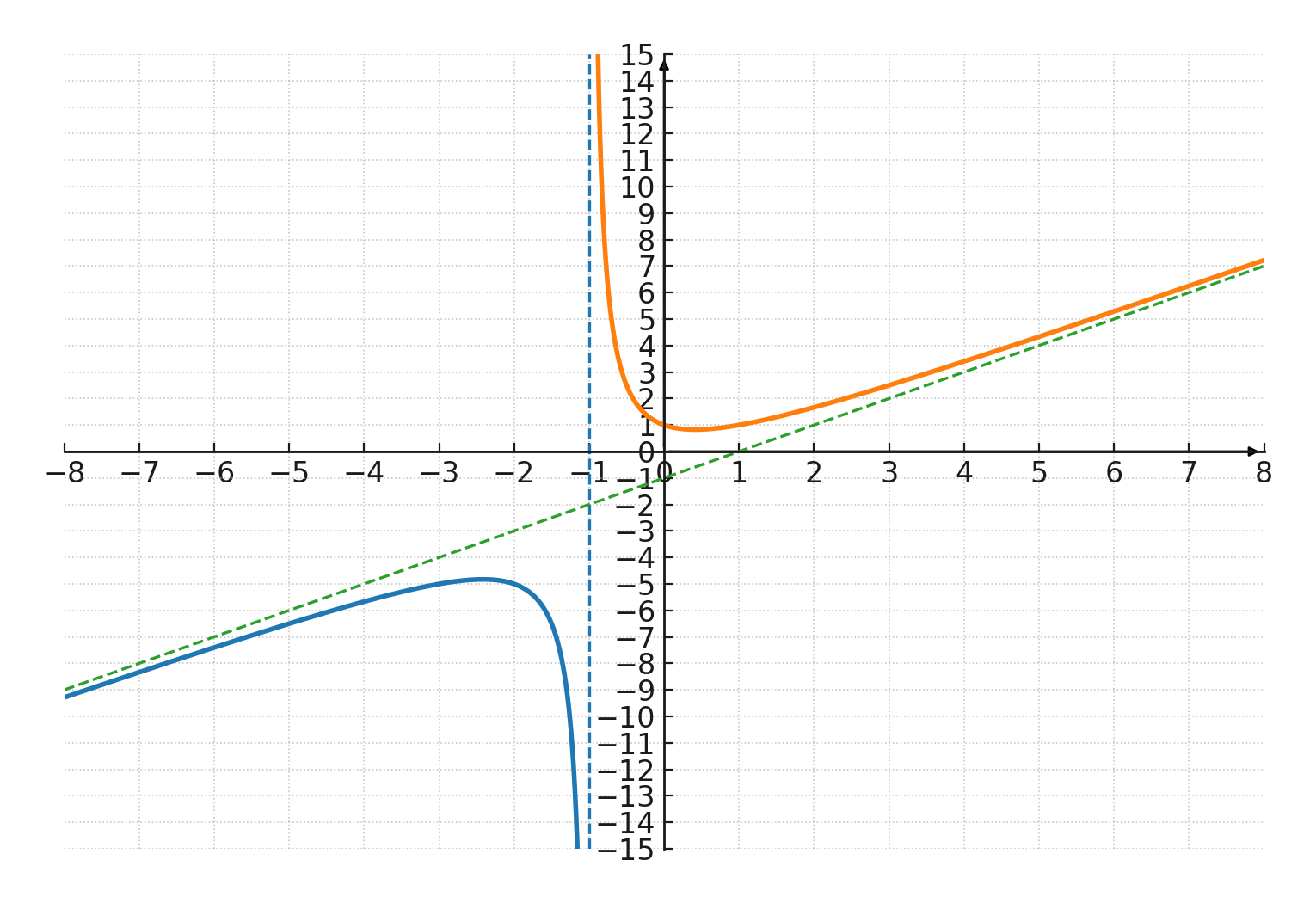
Elles apparaissent lorsque le degré du numérateur est exactement supérieur de 1 à celui du dénominateur.

Par exemple, \(\Large f(x) = \frac{x^2+1}{x+1} \) a une asymptote oblique suivant la droite \(\large y = x - 1 \).

 

 

Les asymptotes nous aident à comprendre le comportement d’une courbe sans la tracer complètement.