Fonction inversement proportionnelle

Une fonction est inversement proportionnelle lorsque la condition suivante est remplie :

 

$$ y \cdot x=k $$

 

C’est-à-dire que si l’on multiplie les deux coordonnées, x et y, le résultat est toujours la même constante (k).

 

Par exemple, les paires de coordonnées suivantes :

 

$$ (1,20) = 1 \cdot 20 = 20 $$

$$ (2,10) = 2 \cdot 10 = 20 $$

$$ (4,5) = 4 \cdot 5 = 20 $$

$$ (5,4) = 5 \cdot 4 = 20 $$

$$ (10,2) = 10 \cdot 2 = 20 $$

$$ (20,1) = 20 \cdot 1 = 20 $$

 

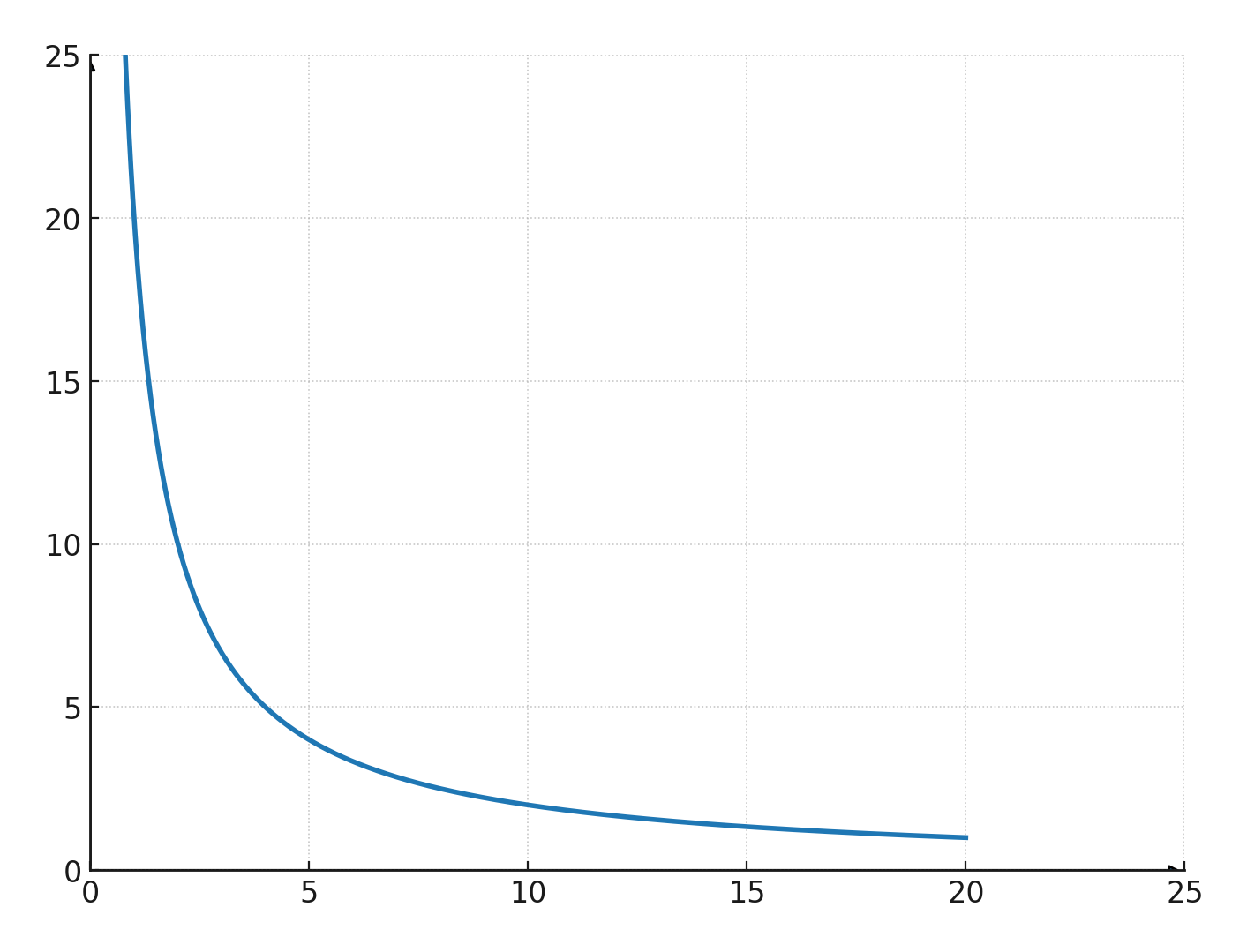
Si l’on trace ces paires de coordonnées dans un système, on obtient la courbe ci-dessous, qui possède toujours des asymptotes le long des deux axes.

Cela signifie qu’elle peut s’approcher très près des axes, mais ne les coupe jamais.

 

 

La constante k

k est appelée la constante de proportionnalité.

L’expression fonctionnelle de la proportionnalité inverse s’écrit ainsi :

 

$$ f_{(x)} = \frac{k}{x} $$

 

\( x \) ne peut pas être 0. On ne peut pas diviser par 0.

Si la constante vaut 15 et x = 5, alors y = 3

 

$$ y = \frac{15}{5} $$

$$ y = 3 $$

 

De cette façon, tu peux calculer d’autres paires de coordonnées avec la même constante (15).

Remarque que si tu as trouvé la coordonnée \((5,3)\), alors \((3,5)\) est aussi valable.

 

Tu peux aussi le faire avec x = -5, alors y = -3

 

$$ y = \frac{15}{-5} $$

$$ y = -3 $$

 

Si tu utilises des nombres négatifs, tu pourras tracer une autre courbe, qui est le miroir de la première.

Ces courbes s’appellent une Hyperbole.

 

Hyperbole

Ci-dessous est tracée une hyperbole avec la constante 15

Les coordonnées de la courbe dans le premier quadrant sont indiquées dans le tableau de valeurs :

 

\(\Large x \)	1	2	3	5	6	10	15
\(\Large y \)	15	7,5	5	3	2,5	1,5	1

 

 

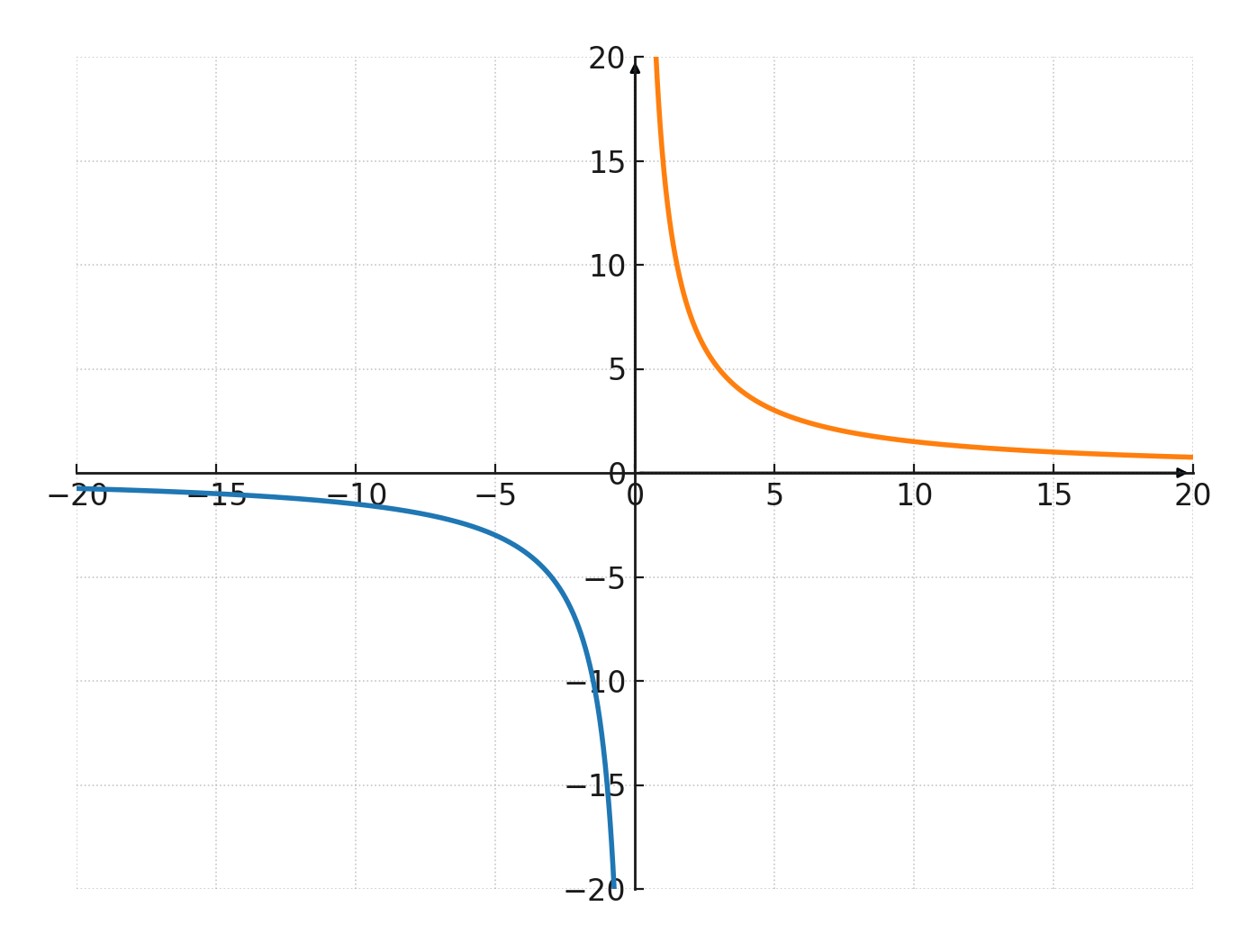
Pour la courbe du troisième quadrant, il est également vrai que \( x \cdot y = 15\)

 

\(\Large x \)	-1	-2	-3	-5	-6	-10	-15
\(\Large y \)	-15	-7,5	-5	-3	-2,5	-1,5	-1

 

Dans cet exemple, certaines coordonnées ont été omises par manque de place. Tu devrais calculer des paires de coordonnées pour tous les x de 1 à 15.

Ainsi, tu pourras tracer une courbe plus précise.