Lineær funktion

En lineær funktion skrives på denne form:

$$ \large f(x)=a \cdot x + b $$

Hvis en lineær funktion tegnes som graf, vil den altid blive til en ret linie.

Grafen kan være stigende, faldende eller vandret afhængigt af $ \large a$ , og $ \large b$ fortæller hvor den skærer y-aksen

$ \large a$ kaldes hældningskoefficienten:

Hvis $ \large a > 0$ er linien stigende fra venstre mod højre
Hvis $ \large a<0$ er linien faldende fra venstre mod højre
Hvis $ \large a = 0$ er linien vandret, fordi uanset hvad $\large x$ er, så er $\large y$ det samme hele tiden.

$ \large b$ fortæller at linien vil skære y-aksen i punktet $(0,b)$

Hvis vi ser på denne funktion:

$$ \large y=2x+5 $$

Så kan vi se at det er en stigende linie, fordi $\large a=2$.

Vi kan også se at den vil skære y-aksen i $(0,5)$, fordi $\large b=5$.

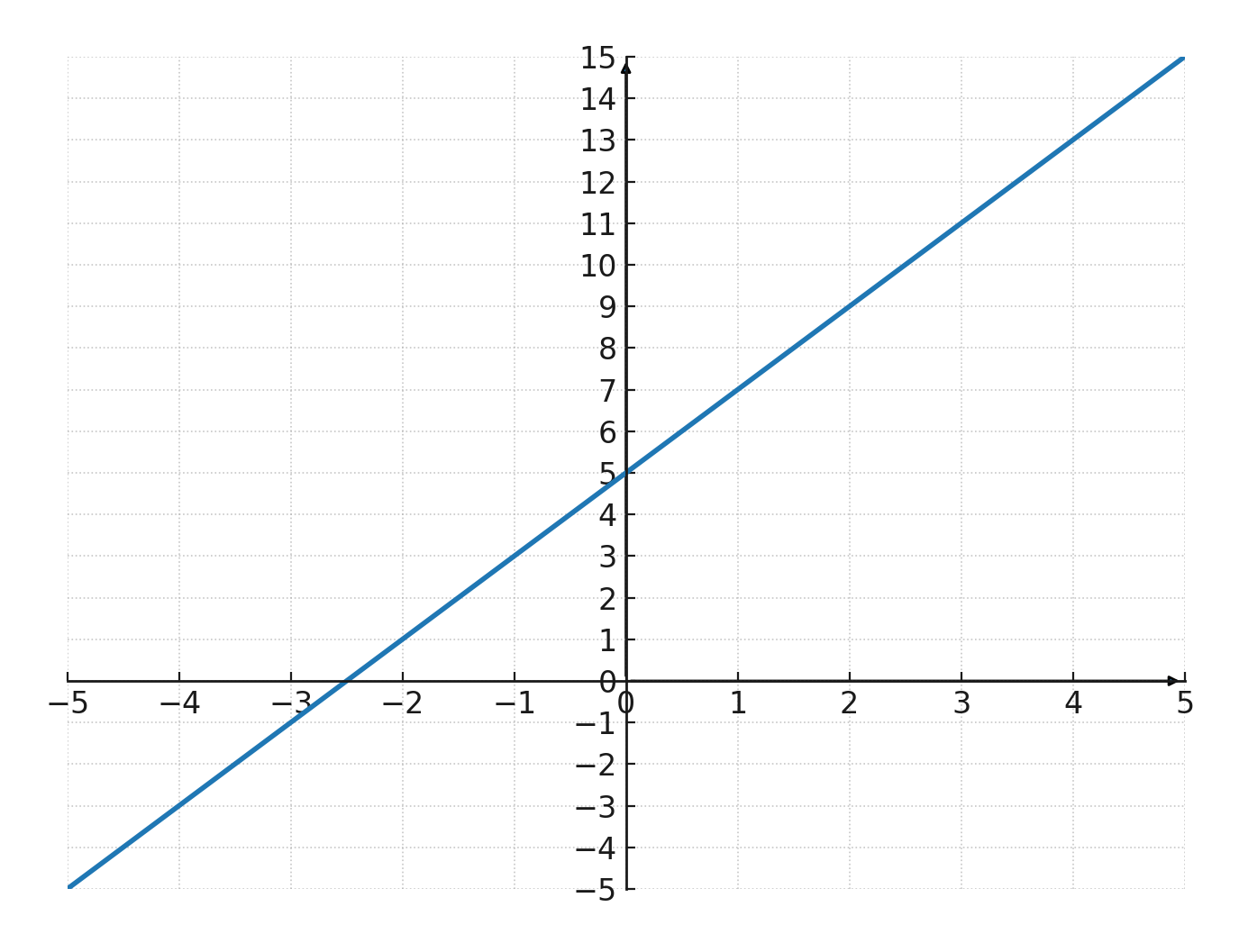
Vi prøver funktionen: $ \large y=2x+5 $

Koordinaterne er indsat i værditabellen herunder og efterfølgende i koordinatsystemet, så grafen kan tegnes:

$\large x$	1	2	3	4	5
$\large y$	7	9	11	13	15

Lineær funktion

Hvis vi har koordinaterne $(2,9)$ og $(4,13)$, er det muligt at finde $\large a$ og $\large b$ på flg. måde:

$$ \large a = \frac{y_2-y_1}{x_2-x_1} \Leftrightarrow $$

$$ \large a = \frac{13-9}{4-2} \Leftrightarrow $$

$$ \large a = \frac{4}{2} \Leftrightarrow $$

$$ \large a = 2 $$

Når vi har fundet $\large a$, kan vi også finde $\large b$, med en af disse to formler. (Det er lige meget hvilken en man bruger)

$$ \large b = y_1 - a \cdot x_1 $$

$$ \large b = y_2 - a \cdot x_2 $$

Vi bruger den første:

$$ \large b = 9 - 2 \cdot 2 \Leftrightarrow $$

$$ \large b = 9 - 4 \Leftrightarrow $$

$$ \large b = 5 $$

Funktionsforskriften for koordinaterne $(2,9)$ og $(4,13)$ er altså

$$ \large y = ax + b $$

$$ \large y = 2x + 5 $$

\(\large x\)	1	2	3	4	5
\(\large y\)	7	9	11	13	15