Trigonometrische Funktionen
Trigonometrische Funktionen sind Funktionen, die auf den Verhältnissen in einem rechtwinkligen Dreieck beruhen. Die drei bekanntesten trigonometrischen Funktionen sind Sinus, Kosinus und Tangens.
Diese Funktionen sind periodisch, was bedeutet, dass sie sich in festen Intervallen wiederholen. Sie spielen eine zentrale Rolle in Mathematik, Physik und Technik, insbesondere im Zusammenhang mit Wellen, Rotationen und Winkeln.
Sinusfunktion
Die Sinusfunktion beschreibt das Verhältnis zwischen der Gegenkathete und der Hypotenuse in einem rechtwinkligen Dreieck.
Sie wird in folgender Form geschrieben:
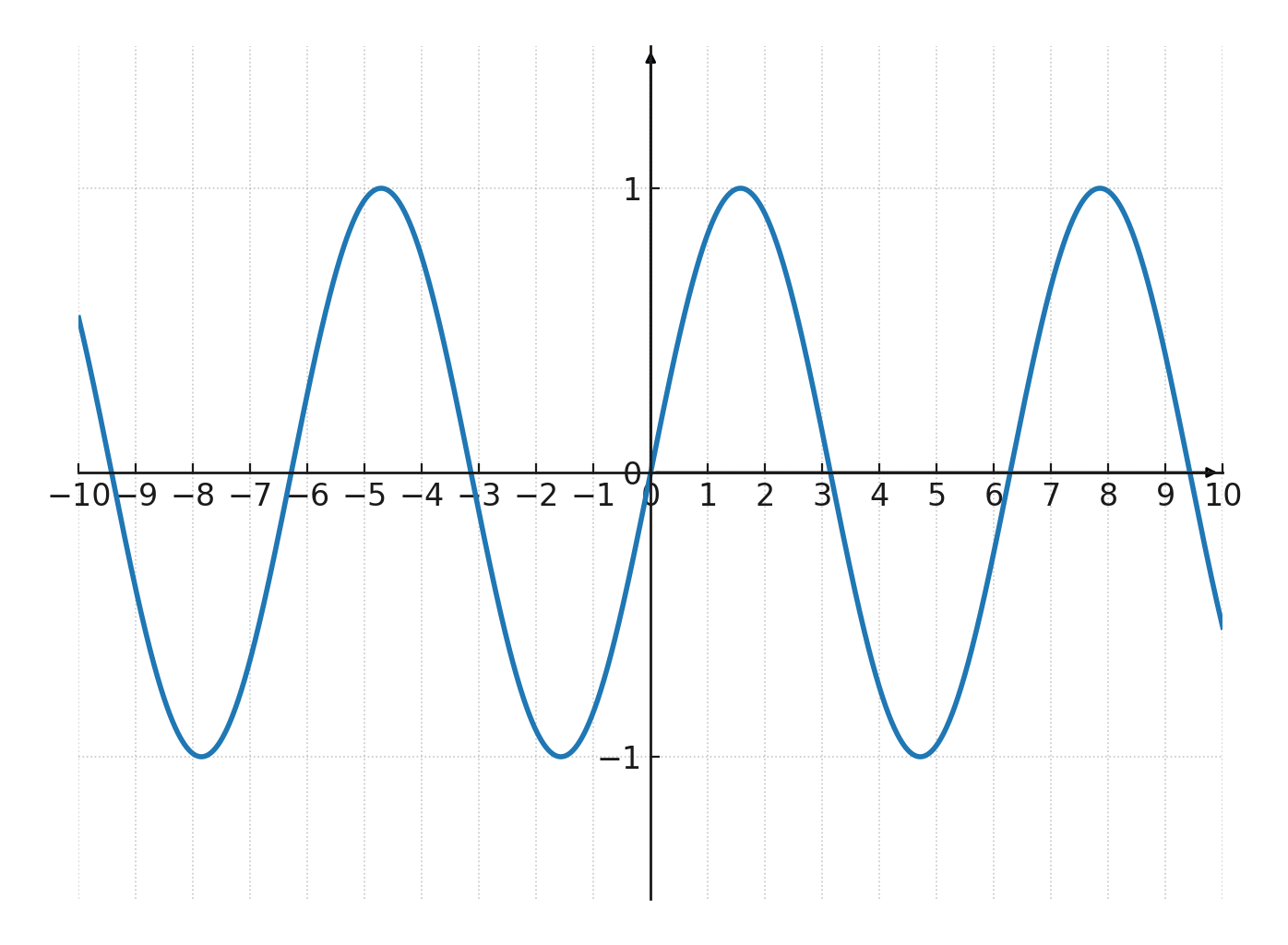
$$ \Large y = \sin(x) $$
Charakteristika:
- Die Periode ist \(2\pi\)
- Die Amplitude ist 1
- Beginnt bei \((0,0)\)
- Die Kurve schwankt zwischen -1 und 1
Beispiel: Werte für \(\large y = \sin(x) \)
| \(\Large x\) | 0 | \(\Large \tfrac{\pi}{2}\) | \(\Large \pi\) | \(\Large \tfrac{3\pi}{2}\) | \(\Large 2\pi\) |
| \(\Large y\) | 0 | 1 | 0 | -1 | 0 |
Kosinusfunktion
Die Kosinusfunktion beschreibt das Verhältnis zwischen der Ankathete und der Hypotenuse in einem rechtwinkligen Dreieck.
Sie wird in folgender Form geschrieben:
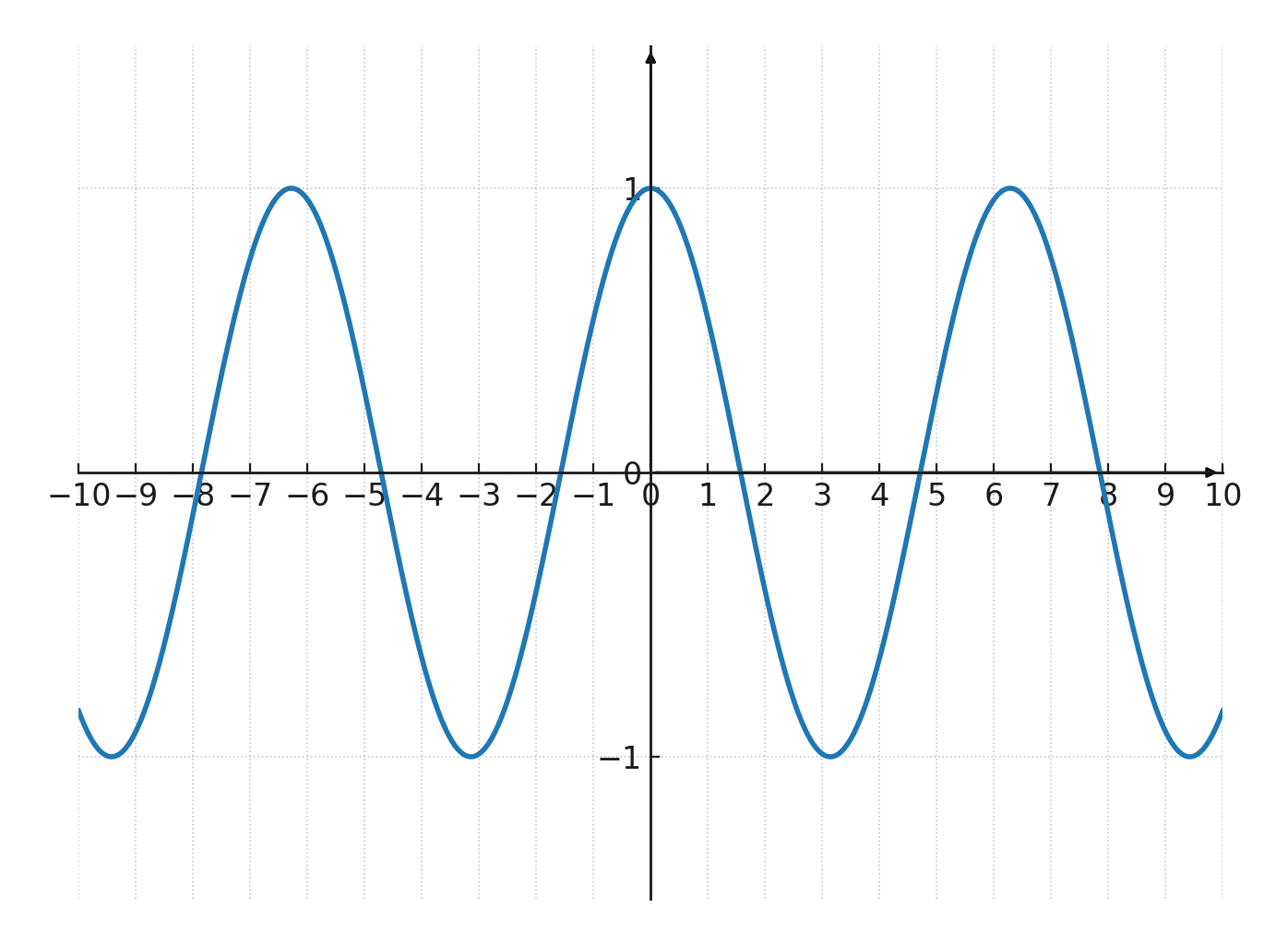
$$ \Large y = \cos(x) $$
Charakteristika:
- Die Periode ist \(2\pi\)
- Die Amplitude ist 1
- Beginnt bei \((0,1)\)
- Die Kurve schwankt zwischen -1 und 1
Beispiel: Werte für \(\large y = \cos(x) \)
| \(\Large x\) | 0 | \(\Large \tfrac{\pi}{2}\) | \(\Large \pi\) | \(\Large \tfrac{3\pi}{2}\) | \(\Large 2\pi\) |
| \(\Large y\) | 1 | 0 | -1 | 0 | 1 |
Tangensfunktion
Die Tangensfunktion beschreibt das Verhältnis zwischen der Gegenkathete und der Ankathete in einem rechtwinkligen Dreieck.
Sie wird in folgender Form geschrieben:
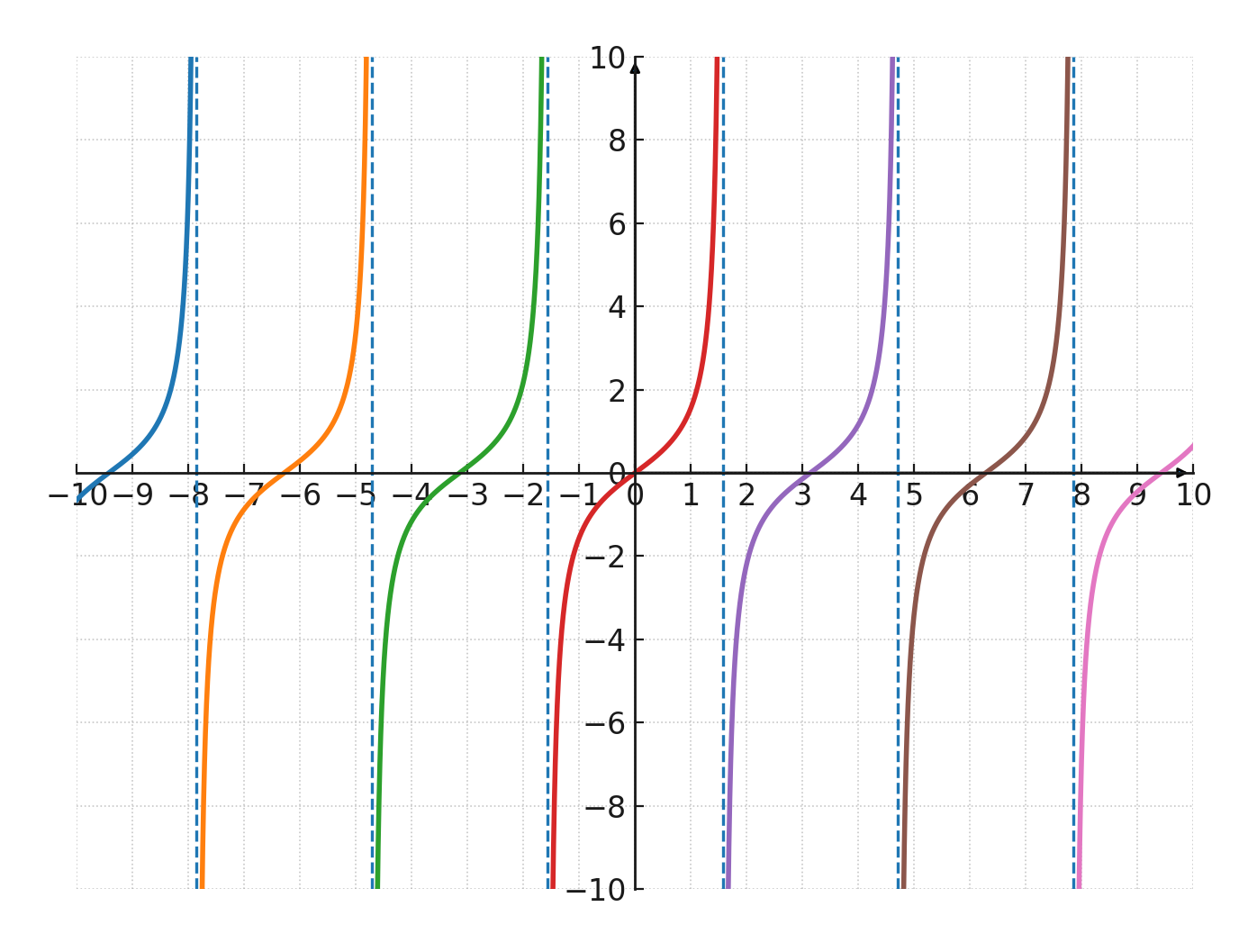
$$ \Large y = \tan(x) $$
Charakteristika:
- Die Periode ist \(\pi\)
- Keine Amplitude (die Funktion kann unendlich groß oder unendlich klein werden)
- Asymptoten bei \( x = \tfrac{\pi}{2}, \tfrac{3\pi}{2}, \ldots \)
- Beginnt bei \((0,0)\)
Beispiel: Werte für \(\large y = \tan(x) \)
| \(\Large x\) | -\(\Large \tfrac{\pi}{4}\) | 0 | \(\Large \tfrac{\pi}{4}\) | \(\Large \tfrac{\pi}{2}\) |
| \(\Large y\) | -1 | 0 | 1 | unendlich |
Zusammenfassung
Sinus, Kosinus und Tangens sind allesamt trigonometrische Funktionen mit unterschiedlichen Eigenschaften, die jedoch miteinander verbunden sind.
- Der Sinus beginnt bei 0 und beschreibt die Auf- und Abwärtsbewegung
- Der Kosinus beginnt bei 1 und ist gegenüber dem Sinus verschoben
- Die Tangensfunktion hat Asymptoten und wiederholt sich mit einer kürzeren Periode
Die drei Funktionen werden häufig zusammen verwendet, um Winkel, Bewegungen und periodische Phänomene in Mathematik und Naturwissenschaften zu beschreiben.