Koordinatensystem

Ein Koordinatensystem besteht aus zwei Zahlenstrahlen, die senkrecht zueinander stehen. Die Zahlenstrahlen werden Achsen genannt.

Die waagerechte Achse wird x-Achse oder erste Achse genannt, und die senkrechte Achse wird y-Achse oder zweite Achse genannt.

Die beiden Achsen schneiden sich in ihrem Nullpunkt. Dieser Punkt wird Ursprung genannt.

 

 

Punkte im Koordinatensystem

Ein Punkt im Koordinatensystem kann abgelesen werden, indem man eine senkrechte Linie zu den Achsen zieht und die Werte der x- und y-Achse an dieser Stelle abliest. Die x-Achse wird immer zuerst gelesen, daher wird ein Punkt als \( \large (x,y)\) beschrieben.

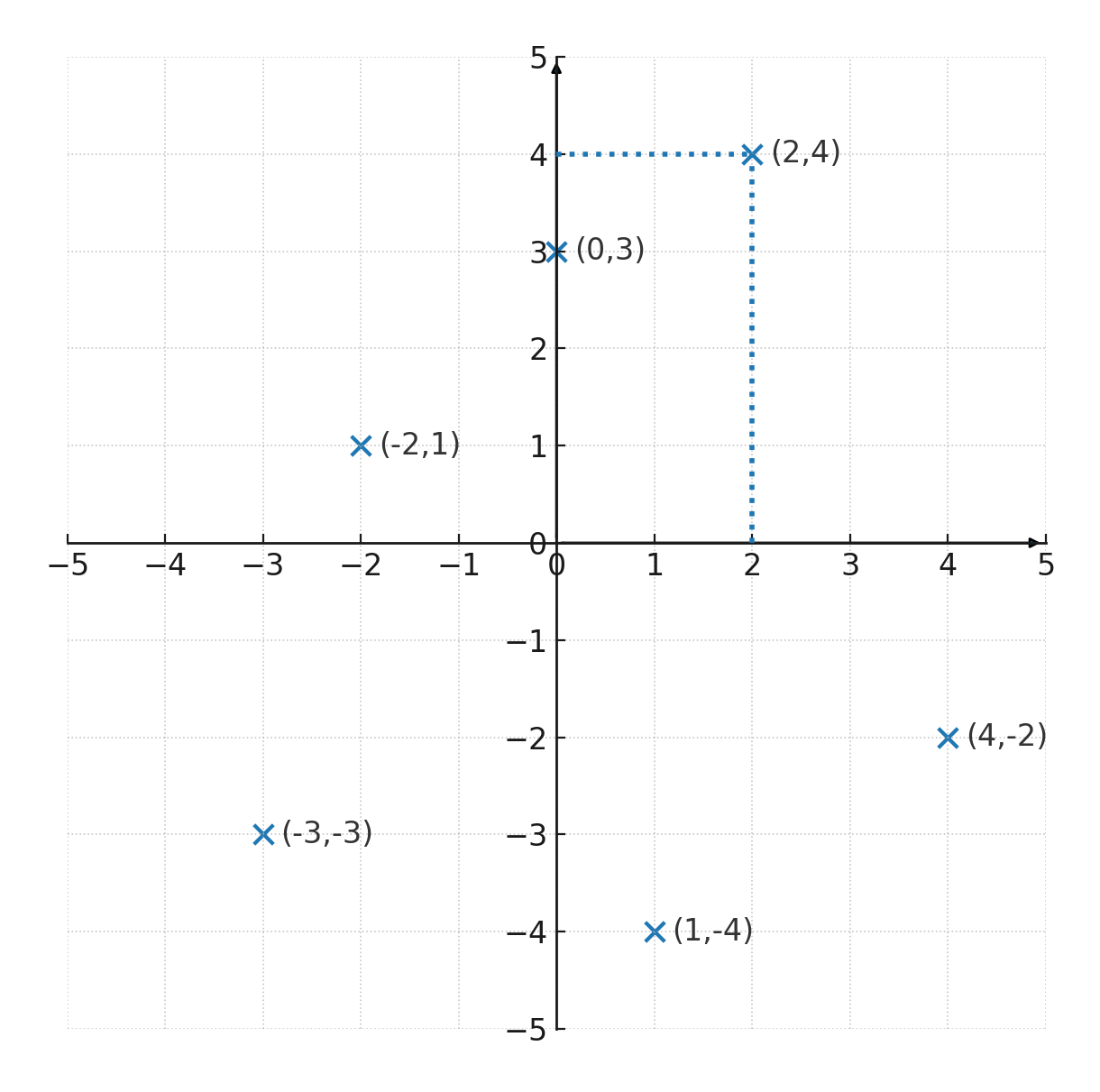
Im folgenden Koordinatensystem sind verschiedene Punkte eingezeichnet.

Der Punkt \( \large (2,4)\) liegt im Koordinatensystem, wobei die beiden senkrechten Linien zeigen, dass:

• x-Achse = 2
• y-Achse = 4

 

 

 

Quadranten

Die vier Bereiche im Koordinatensystem werden Quadranten genannt, wobei:

 

• 1. Quadrant: \( \large (x,y)\)
• 2. Quadrant: \( \large (-x,y)\)
• 3. Quadrant: \( \large (-x,-y)\)
• 4. Quadrant: \( \large (x,-y)\)

 

Drei Dimensionen

Das Koordinatensystem kann auch auf drei Dimensionen erweitert werden, indem eine z-Achse hinzugefügt wird, die im Ursprung senkrecht zur x- und y-Achse steht.

Im zweidimensionalen System gibt es vier Quadranten, aber im dreidimensionalen System wird der Raum in acht Bereiche unterteilt, die Okktanten genannt werden.

Punkte werden mit drei Zahlen angegeben \( (x,y,z) \). Dies wird zum Beispiel in der Raumgeometrie verwendet.