Polynome

Ein Polynom ist eine spezielle Art mathematischer Funktion, die aus Termen besteht, in denen eine Variable (meist x genannt) mit verschiedenen Potenzen versehen und mit Zahlen (Koeffizienten) multipliziert wird. Schließlich können mehrere dieser Terme addiert werden.

 

Die einfachste Art von Polynom ist eine konstante Funktion. Sie wird ein Polynom 0. Grades genannt, weil kein x vorkommt. Die Funktion hat immer denselben Wert, egal was x ist.

Ein Beispiel ist:

 

$$ \large f(x) = 5 $$

 

Hier ist der Wert immer 5, egal ob x -10, 0 oder 100 ist. Der Graph ist daher eine horizontale Linie parallel zur x-Achse.

 

Hier ein Beispiel für ein Polynom 2. Grades. Es wird auch quadratische Funktion genannt:

 

$$ \large f(x) = 2x^2 + 3x + 1 $$

 

Hier gibt es drei Terme: \(2x^2\), \(3x\) und \(1\). Zeichnet man dies als Graph, ergibt sich eine Parabel:

 

 

 

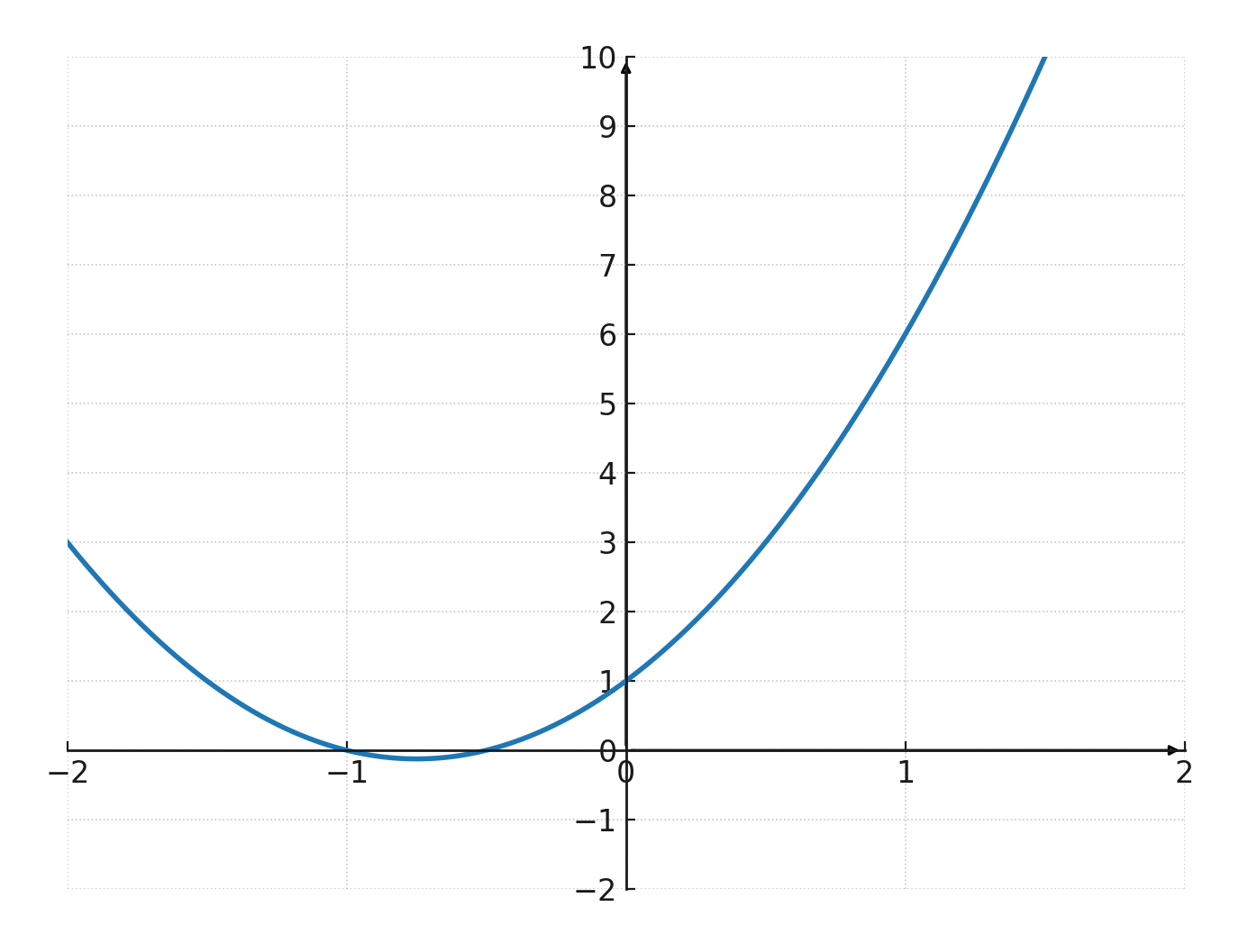
Der Grad eines Polynoms

Die höchste Potenz von x (der Exponent) wird der Grad des Polynoms genannt:

 

• 0. Grad: Konstante Funktion, z. B. \( f(x)=5 \).
• 1. Grad: Lineare Funktion, z. B. \( f(x)=2x+1 \).
• 2. Grad: Quadratische Funktion, z. B. \( f(x)=x^2-3x+2 \).
• 3. Grad: Kubische Funktion, z. B. \( f(x)=x^3-3x+2 \).

 

Ab dem 4. Grad und höher verwendet man normalerweise einfach die Bezeichnung Polynom n-ten Grades anstelle eines besonderen Namens.

 

Je höher der Grad, desto komplexer werden die Graphen, und die Kurven können sich auf mehrere Arten biegen.

 

Eine unendliche Familie

Polynome bilden eine ganze Familie von Funktionen.

Es gibt Polynome aller Grade, und deshalb kann man sagen, dass es im Prinzip eine unendliche Reihe von Funktionen ist. Jedes Polynom hat seinen eigenen speziellen Graphen, abhängig vom Grad und den verwendeten Koeffizienten.

 

Wo werden Polynome verwendet?

Polynome sind wichtig, weil sie in vielen Bereichen der Mathematik und des wirklichen Lebens vorkommen:

 

• In der Wirtschaft kann eine Funktion die Entwicklung von Zinsen oder Investitionen beschreiben.
• In der Physik kann eine Funktion eine Bewegung oder Geschwindigkeit beschreiben.
• In der Statistik helfen sie, Kurven an Daten anzupassen.

 

Auch wenn Polynome technisch klingen, sind sie grundlegende Bausteine der Mathematik und geben uns Werkzeuge, um von einer einfachen Geraden bis zu viel komplexeren Zusammenhängen alles zu beschreiben und zu verstehen.