Kubische Funktion

Eine kubische Funktion ist eine Funktion dritten Grades. Die allgemeine Vorschrift lautet:

 

$$ \large f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d $$

 

Hier gilt \( \large a \neq 0\), andernfalls würde mit 0 multipliziert und die Funktion würde zu einer quadratischen Funktion.

 

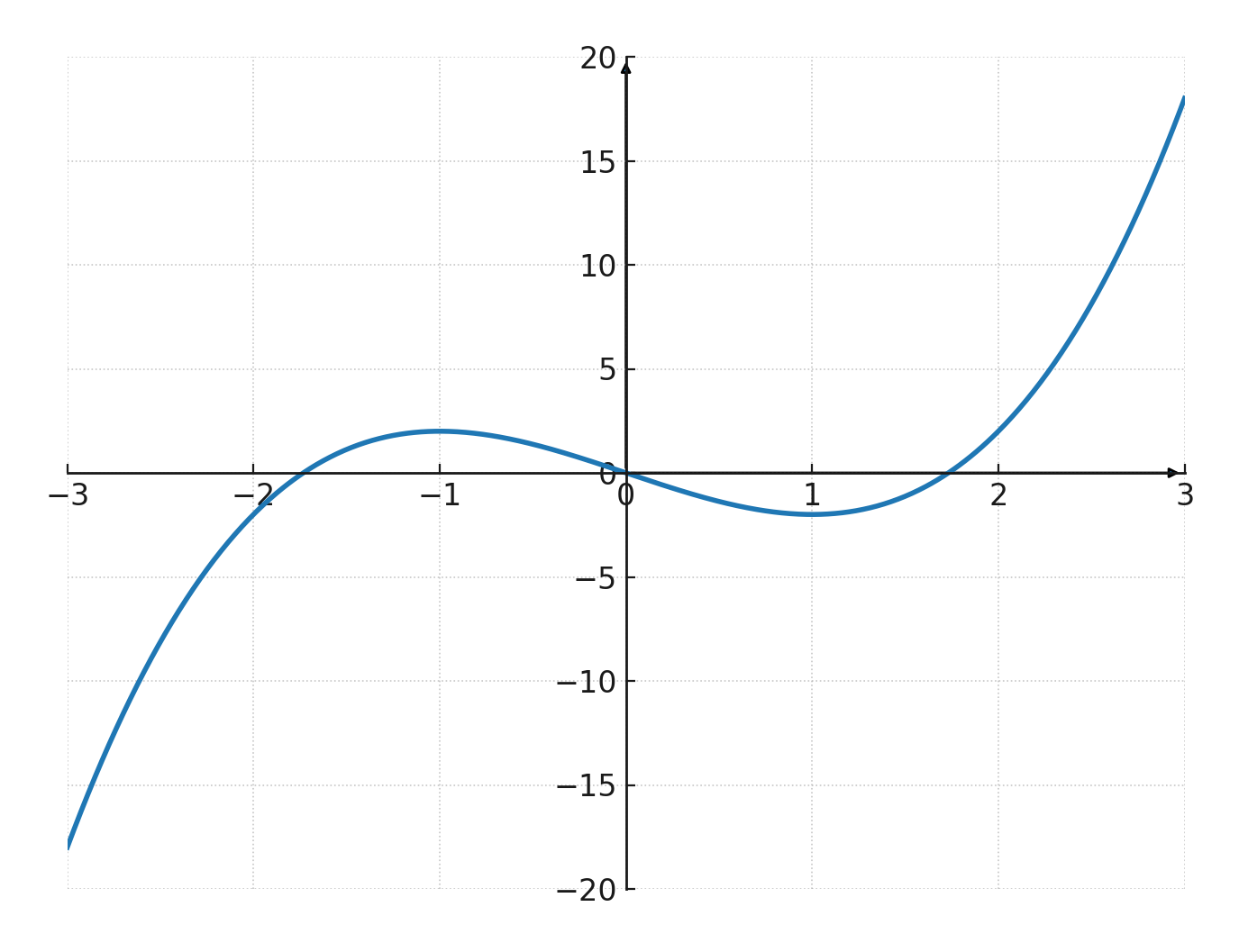
Der Graph einer kubischen Funktion wird kubische Kurve genannt. Er hat typischerweise eine S-Form, kann jedoch je nach Koeffizienten variieren.

 

• Wenn \( \large a > 0\), beginnt der Graph unten links und endet oben rechts.
• Wenn \( \large a < 0\), beginnt der Graph oben links und endet unten rechts.

 

 

Nullstellen

Eine kubische Funktion kann je nach Diskriminante einen oder drei Schnittpunkte mit der x-Achse haben.

Eine Nullstelle ist der Punkt, an dem sie die x-Achse schneidet oder berührt, also dort, wo \( \large f(x) = 0 \). Sie hat daher immer mindestens eine reelle Nullstelle und kann bis zu drei reelle Nullstellen haben.

 

Hoch- und Tiefpunkte

Eine kubische Funktion kann sowohl ein lokales Maximum (Hochpunkt) als auch ein lokales Minimum (Tiefpunkt) haben, wenn die Diskriminante dies zulässt. In diesem Fall erhält der Graph seine charakteristische S-Form.

Wenn die Bedingungen nicht erfüllt sind, steigt oder fällt der Graph einfach durchgehend ohne Krümmung.

 

Weitere wichtige Punkte

• Der Graph schneidet die y-Achse im Punkt \( \large (0,d)\)
• Der Graph hat immer einen Wendepunkt bei \( \large x=-\frac{b}{3a}\)
• Man kann die Form des Graphen mit dem Ausdruck \( \large b^2 - 3ac \) bestimmen
  • Wenn \( \large b^2-3ac>0\), gibt es zwei Extrempunkte (einen Hoch- und einen Tiefpunkt).
  • Wenn \( \large b^2-3ac=0\), gibt es einen doppelten stationären Punkt.
  • Wenn \( \large b^2-3ac<0\), gibt es keine Extrempunkte.

 

Beispiel

Wir probieren mit folgender Funktion:

 

$$ \large f(x) = x^3 - 3x + 2 $$

 

Hier gilt \( \large a = 1\), \( \large b = 0\), \( \large c = -3\), \( \large d = 2\).

 

Die Funktion ergibt folgende Koordinaten:

\( x \)	-2	-1	0	1	2	3
\( y \)	-4	4	2	0	4	20

 

 

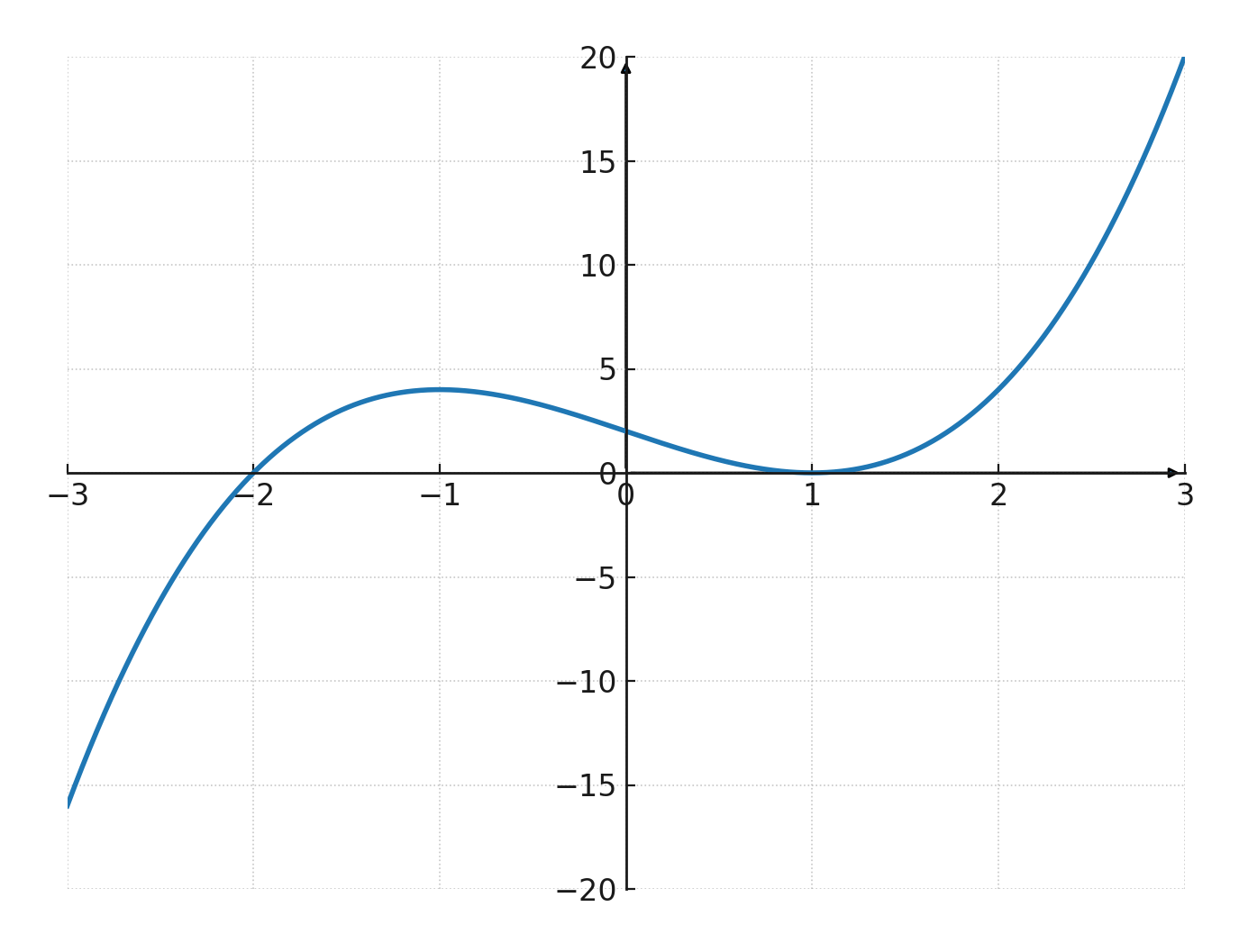
Es ist möglich, die Funktion zu faktorisieren:

$$ \large f(x) = (x+2)(x-1)^2 $$

 

Daraus folgt, dass der Graph die Nullstellen \( \large (-2,0)\) und \( \large (1,0)\) hat. Der Punkt \( \large (1,0)\) ist eine doppelte Nullstelle, was bedeutet, dass der Graph die x-Achse hier berührt, ohne sie zu schneiden.

Wenn er sie stattdessen geschnitten hätte, hätte die Funktion drei verschiedene Nullstellen.

 

Der Graph schneidet die y-Achse im Punkt \( \large (0,2)\).

 

Die Diskriminante ergibt \( \large b^2 - 3ac = 0^2 - 3 \cdot 1 \cdot (-3) = 9 > 0\), also hat die Funktion sowohl ein lokales Maximum als auch ein lokales Minimum. Deshalb erhält der Graph die klassische S-Form.