Rationale Funktionen

Eine rationale Funktion ist ein Bruch, bei dem sowohl Zähler als auch Nenner Polynome sind. Man kann eine rationale Funktion also schreiben als:

$$ \large f(x) = \frac{P(x)}{Q(x)} $$

Hier sind $P(x)$ und $Q(x)$ Polynome, und der Nenner $Q(x)$ darf nicht gleich 0 sein.

Rationale Funktionen können vertikale Asymptoten haben, dort wo der Nenner 0 wird, und sie können horizontale oder schräge Asymptoten haben, abhängig vom Grad des Zählers und des Nenners.

Beispiel einer rationalen Funktion

Ein Beispiel für eine rationale Funktion ist:

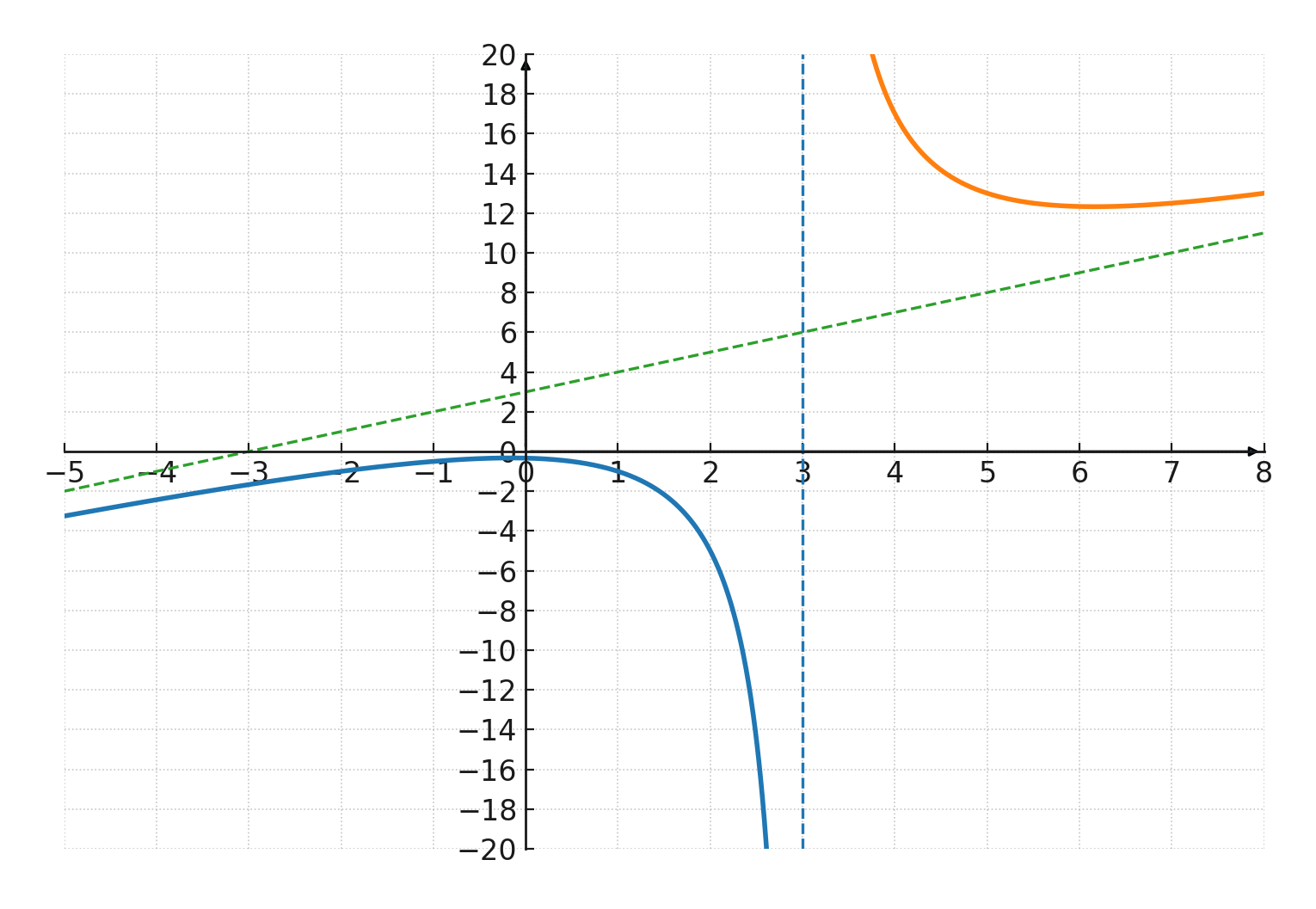
$$ \large f(x) = \frac{x^2+1}{x-3} $$

In diesem Beispiel ist der Zähler $x^2+1$, ein Polynom 2. Grades, und der Nenner $x-3$, ein Polynom 1. Grades.

Die Funktion ist für $x=3$ nicht definiert, weil man nicht durch 0 teilen darf.
Der Graph hat daher eine vertikale Asymptote bei $x=3$.
Wenn $x$ sehr groß oder sehr klein wird, verhält sich der Bruch ungefähr wie $\tfrac{x^2}{x} = x$. Daher hat der Graph eine schräge Asymptote nahe der Geraden $y=x$.

Rationale Funktion

Umgekehrte Proportionalität

Eine der einfachsten Arten rationaler Funktionen ist die umgekehrte proportionale Funktion:

$$ \large f(x) = \frac{k}{x} $$

Hier ist $k$ eine Konstante. Die Funktion ist für $x=0$ nicht definiert, da man nicht durch null teilen kann.

Der Graph hat eine charakteristische Form: er liegt im 1. und 3. Quadranten, wenn $k$ positiv ist, und im 2. und 4. Quadranten, wenn $k$ negativ ist.

Diese Funktion heißt umgekehrt proportional, weil wenn $x$ doppelt so groß wird, $f(x)$ halb so groß wird. Das Produkt $x \cdot f(x)$ ist immer dasselbe (gleich $k$).