Asymptoten

Eine Asymptote ist eine Linie, der sich der Graph einer Funktion immer mehr annähert, ohne sie jemals zu schneiden (oder nur in einzelnen Punkten). Bei rationalen Funktionen sind Asymptoten sehr häufig.

 

Es gibt drei Arten von Asymptoten:

 

Vertikale Asymptoten:

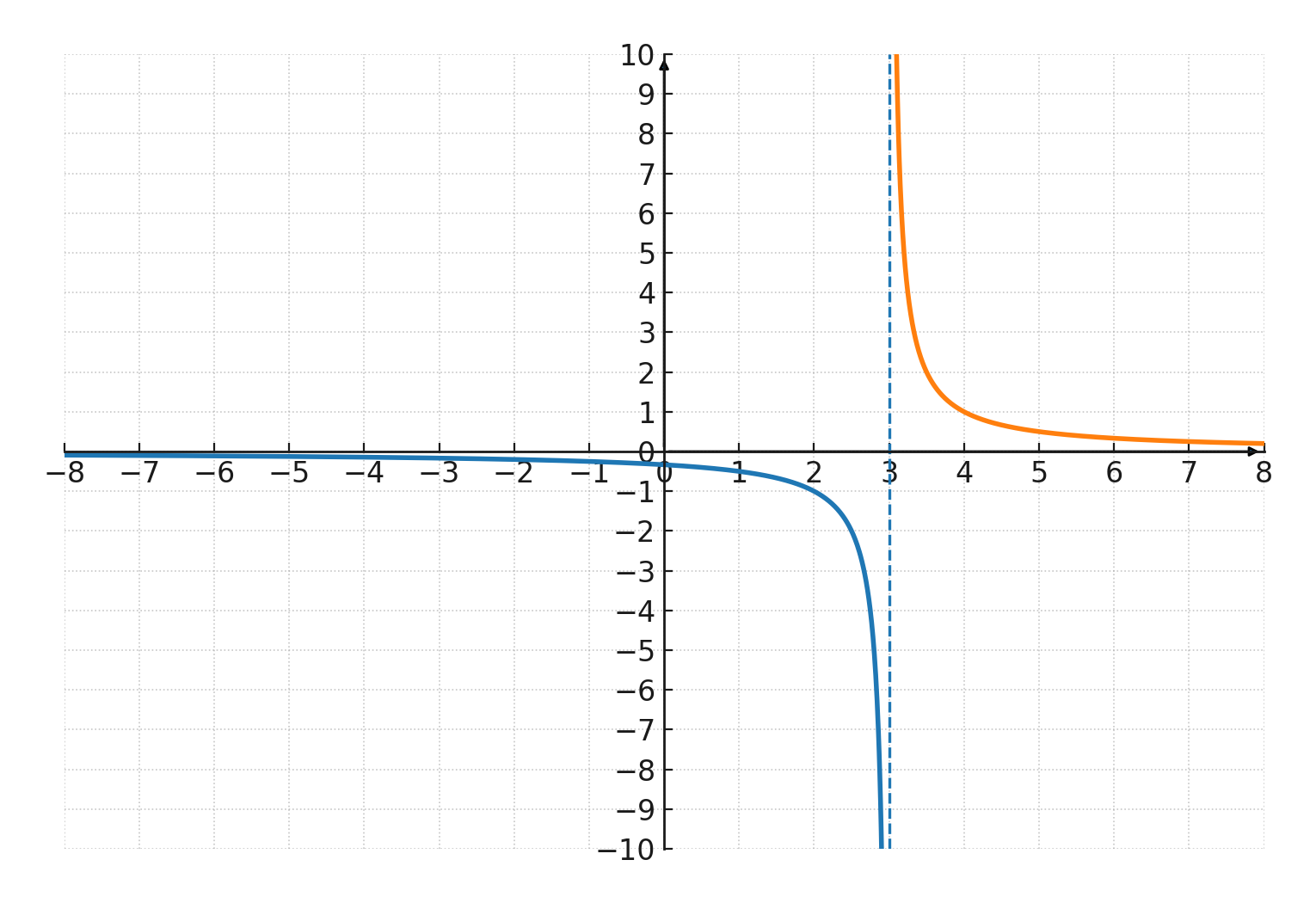
Treten auf, wenn der Nenner einer rationalen Funktion 0 wird. Zum Beispiel hat die Funktion \( \Large f(x) = \frac{1}{x-3} \) eine vertikale Asymptote bei \(\large x = 3 \).

Die Funktion hat außerdem die x-Achse als horizontale Asymptote.

 

Horizontale Asymptoten:

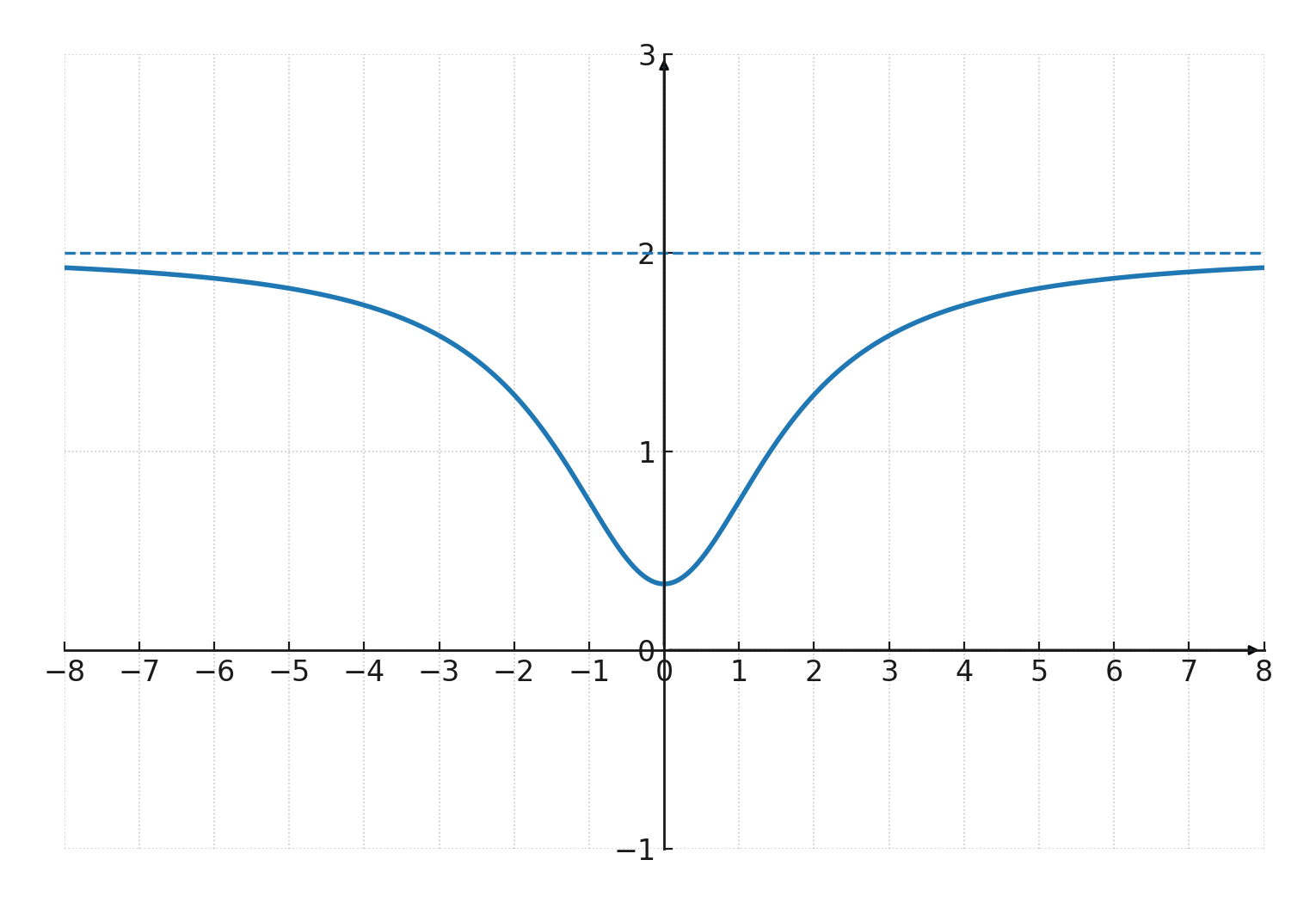
Treten auf, wenn sich der Graph einer Funktion einem konstanten Wert nähert, wenn \(\large x \) sehr groß oder sehr klein wird.

Zum Beispiel hat \(\Large f(x) = \frac{2x^2+1}{x^2+3} \) eine horizontale Asymptote bei \(\large y = 2 \).

 

 

Schiefe Asymptoten:

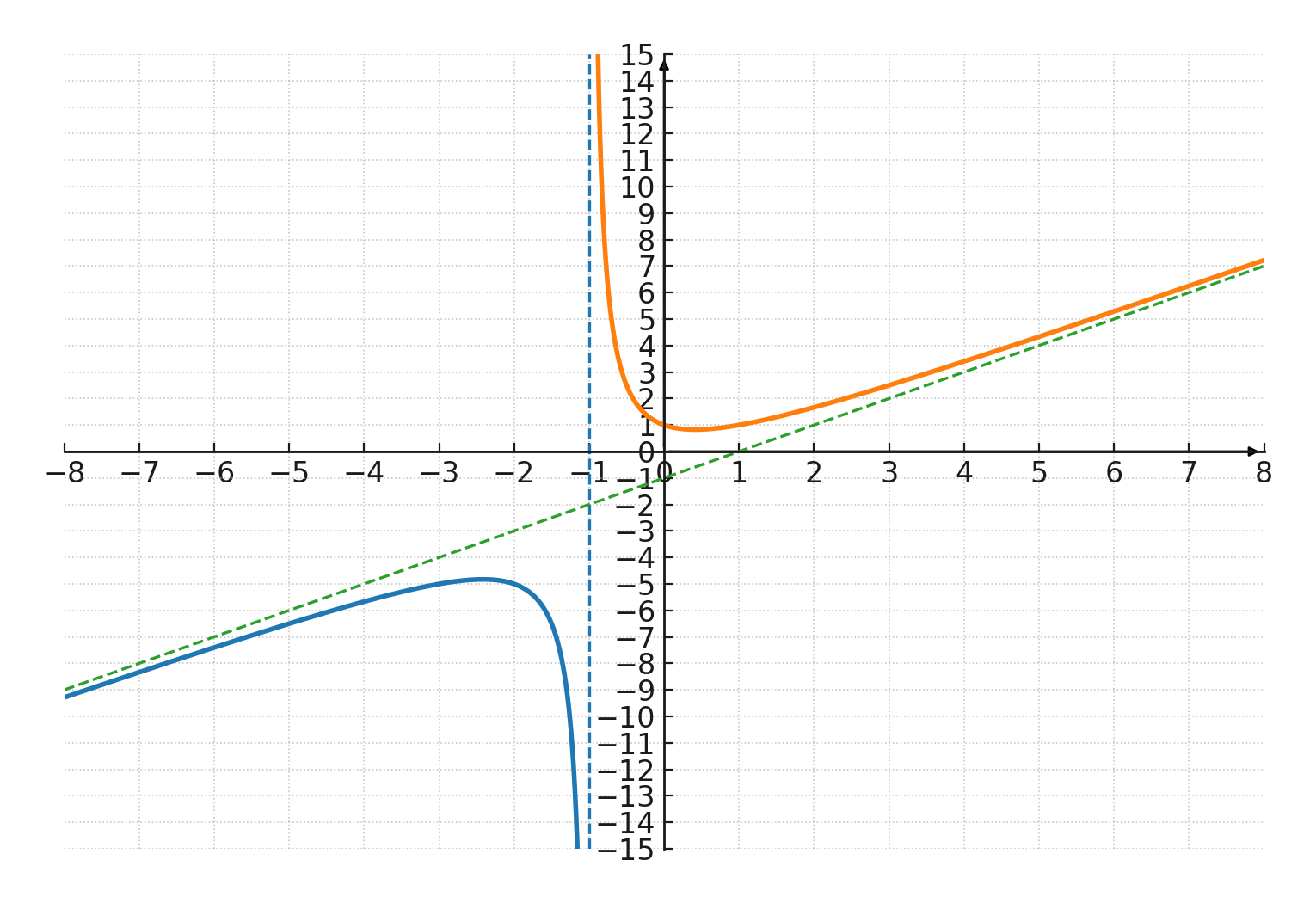
Treten auf, wenn der Grad des Zählers genau 1 höher ist als der Grad des Nenners.

Zum Beispiel hat \(\Large f(x) = \frac{x^2+1}{x+1} \) eine schiefe Asymptote entlang der Geraden \(\large y = x - 1 \).

 

 

Asymptoten helfen uns, das Verhalten eines Graphen zu verstehen, ohne ihn vollständig zu zeichnen.