Bruchfunktionen

Eine Bruchfunktion ist ein Synonym für eine rationale Funktion.

Das heißt, eine Funktion, die geschrieben wird als:

$ \large f(x) = \frac{P(x)}{Q(x)} $

Bei der Analyse einer Bruchfunktion geht man typischerweise in dieser Reihenfolge vor:

Zuerst bestimmt man die Definitionsmenge, dann die Nullstellen, anschließend den Schnittpunkt mit der y-Achse und schließlich die Asymptoten.

Dies ergibt eine zusammenhängende Beschreibung des Graphen.

Definitionsmenge:

Die Definitionsmenge ist die Menge aller erlaubten x-Werte der Funktion.

Für eine Bruchfunktion ist die Definitionsmenge alle reellen x, bei denen $\large Q(x)\neq 0 $.

Wenn sowohl Zähler als auch Nenner an derselben Stelle 0 werden (gemeinsamer Faktor), ist der Punkt dennoch aus der Definitionsmenge ausgeschlossen und erscheint als Lücke im Graphen.

Wenn $\large Q(x)=0 $ aber $\large P(x)\neq 0 $, erhält man typischerweise eine vertikale Asymptote.

Nullstellen:

Der Graph hat Nullstellen an den Punkten, an denen der Zähler 0 ist, sofern der Nenner an derselben Stelle nicht ebenfalls 0 ist.

Schnittpunkt mit der y-Achse:

Er wird gefunden, indem man $ \large x = 0 $ einsetzt, falls dies innerhalb der Definitionsmenge liegt.

Asymptoten:

Vertikale Asymptoten treten typischerweise bei den $ \large x $-Werten auf, bei denen der Nenner 0 ist. Horizontale oder schräge Asymptoten findet man durch den Vergleich der Grade von Zähler und Nenner oder durch Polynomdivision.

Ein Beispiel ist die Funktion:

$$ \large f(x) = \frac{x^2 - 1}{x^2 - 4} $$

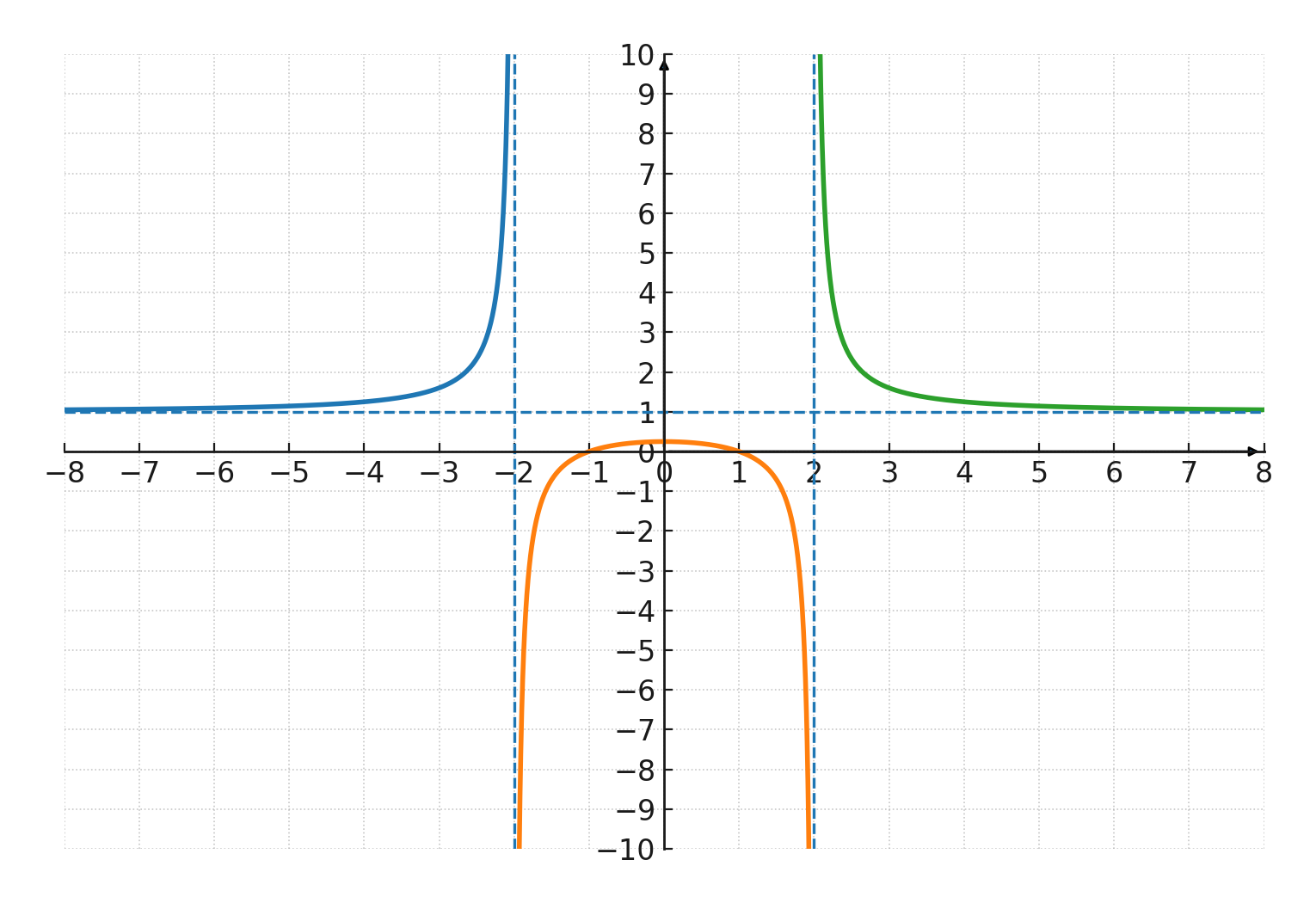
Rationale Funktion mit mehreren vertikalen Asymptoten

Hier ist der Zähler $ \large x^2 - 1 $, was Nullstellen bei $ \large x = 1 $ und $ \large x = -1 $ ergibt.

Der Nenner $ \large x^2 - 4 $ wird bei $ \large x = -2 $ und $ \large x = 2 $ null, daher ist die Funktion dort nicht definiert.

Die Definitionsmenge ist also alle reellen $ \large x $ außer $ \large -2 $ und $ \large 2 $. Der Graph hat vertikale Asymptoten bei $ \large x = -2 $ und $ \large x = 2 $.

Da der Grad von Zähler und Nenner gleich ist, ergibt sich eine horizontale Asymptote bei $ \large y = 1 $. Der Schnittpunkt mit der y-Achse ergibt sich bei $ \large x = 0 $: $ \large f(0) = \frac{-1}{-4} = \frac{1}{4} $.

Mit dieser Vorgehensweise erhält man einen Gesamtüberblick über das Verhalten von Bruchfunktionen.